对于这样的微分方程：
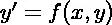
其中，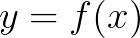
，我们称为常微分方程。
求解常微分方程是有明确的几何意义的。我们下面就通过它的几何意义，来观察什么是通解、特解以及所有解。
一、解常微分方程的几何意义
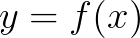是有明确的几何意义的：
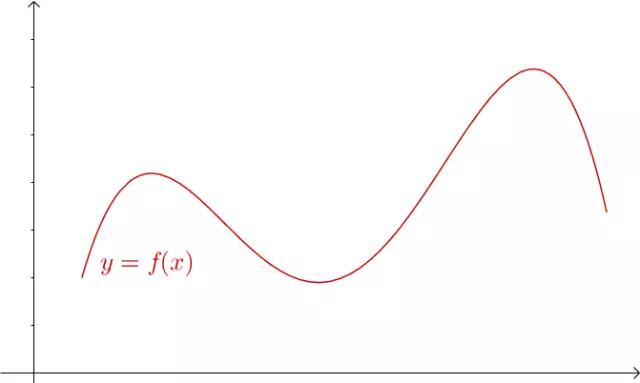
图1
在这个曲线上取几个点，作出点附近的切线：
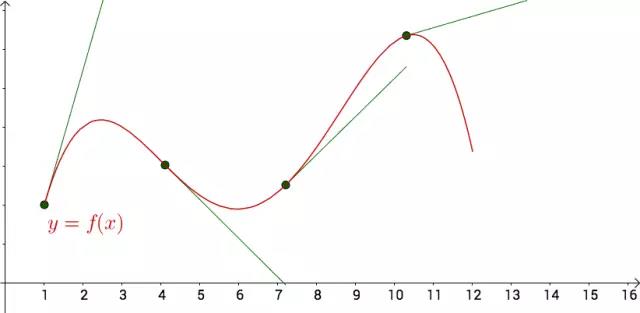
图2
根据微积分的思想，“以直代曲”，切线就是代替曲线的最佳直线。
所以我们可以看到，如果曲线上的点密集一点，切线就看起来很接近曲线了：
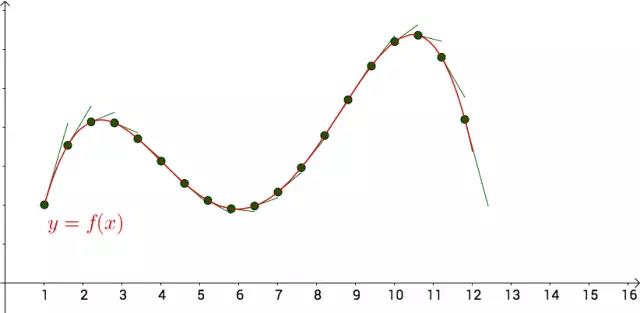
图3
我要是把曲线去掉，你大概也能根据切线脑补出曲线的样子：
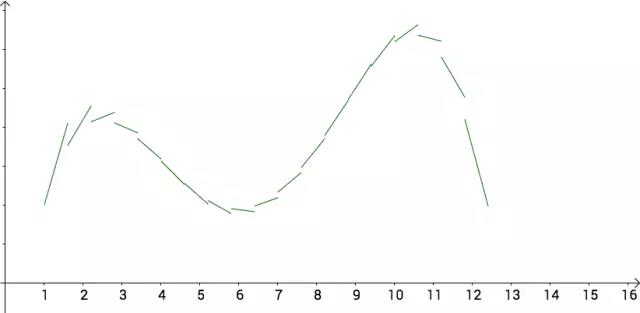
图4
求解常微分方程的几何意义就是，根据切线画出曲线。
二、欧拉方法
欧拉，给出了一个以他名字命名的欧拉方法，可以通过切线来画出曲线。
怎么作出切线呢？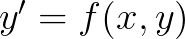
这个就是导数的方程，把导数作为斜率就可以画出切线。
我们举个最简单的例子吧，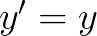
。我们随便选一点作为起始点
：
图5
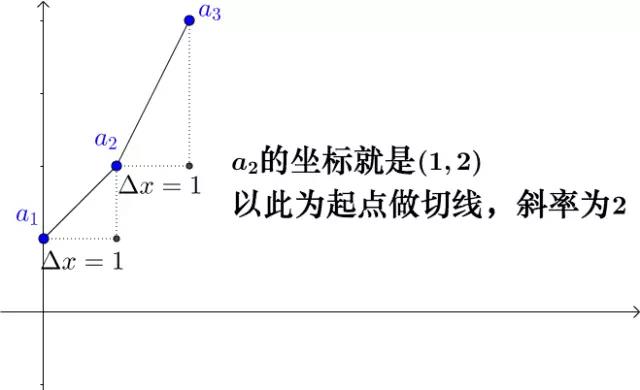
图6
不断重复以上步骤，我们可以得到一个折线段：
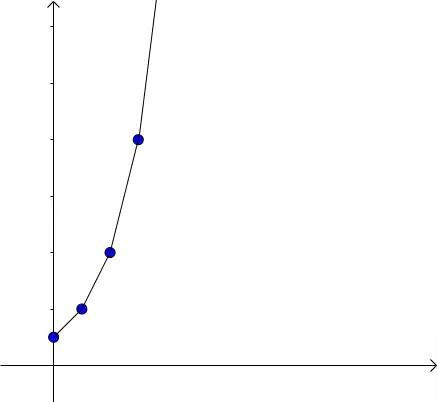
图7
容易知道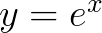
是
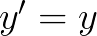的一个解，我把
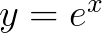画出来看一下，会发现这两个的图像还是有点接近：
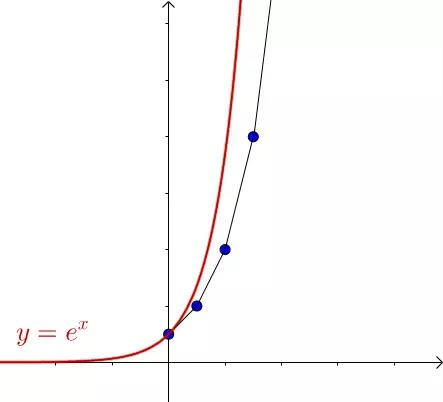
图8
随着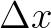
的缩小，图像就越来越接近（为了方便观看，我把点给去掉了）：
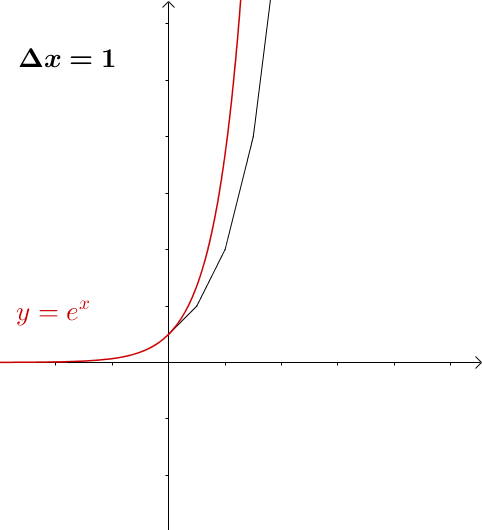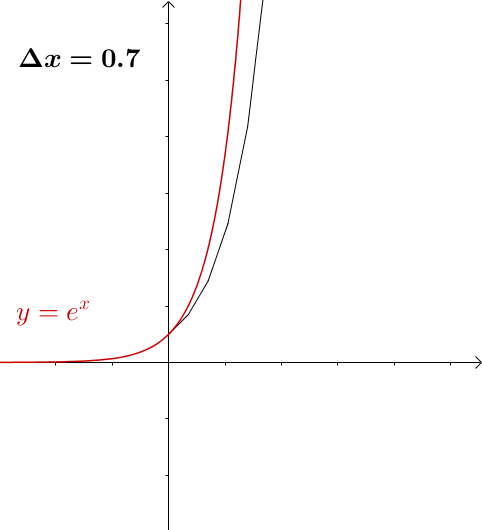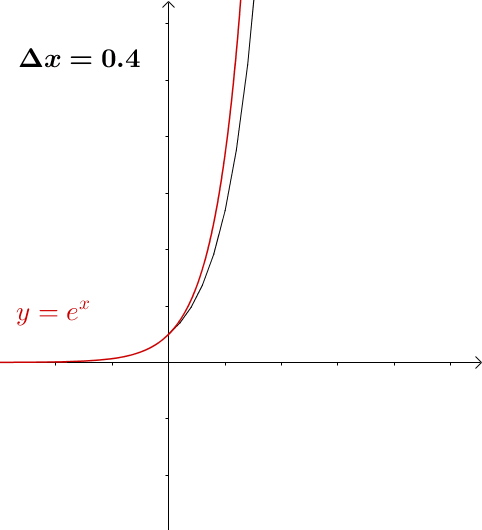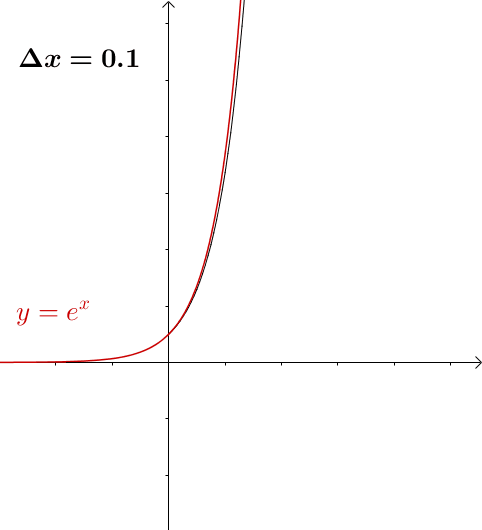
图9
欧拉方法就是这样通过切线来把原来的曲线描绘出来的，这些连起来的折线，我们就称为欧拉折线。
欧拉折线肯定和曲线是有误差的，就好像泰勒级数和原来的曲线有误差一样，这里就不深入讨论了。
三、线素场
欧拉方法计算量其实还蛮大的（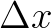
越小计算量越大），不过好歹人手还可以算。
有了计算机之后，我们就可以不管计算量了，所以就有了更有效的线素场。
其实说来也简单，我在平面上等距离取点：
图10
然后以这些点为起点，根据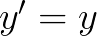
画出切线，这就是线素场（或者称为斜率场）：
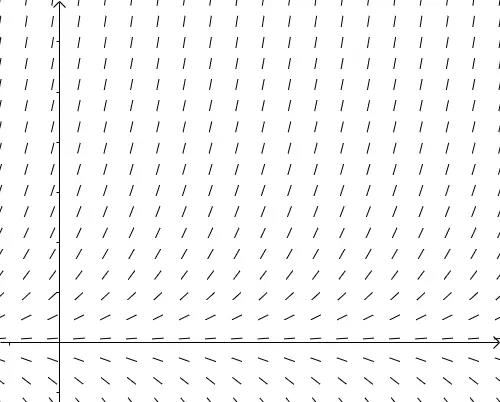
图11
结合欧拉折线和线素场，我们就可以开始分析通解、特解和所有解了。
四、通解、特解和所有解
1. 通过欧拉折线来观察解
我们通过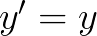
来继续讲解。这个微分方程的通解还是很容易求的，就是：
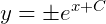
知道通解之后我们通过图像来验证下。
指定
的位置，可以画出不同的欧拉折线（大家可以观察到，有了线素场之后，就算没有欧拉折线，我们大概也可以脑补曲线的样子）：
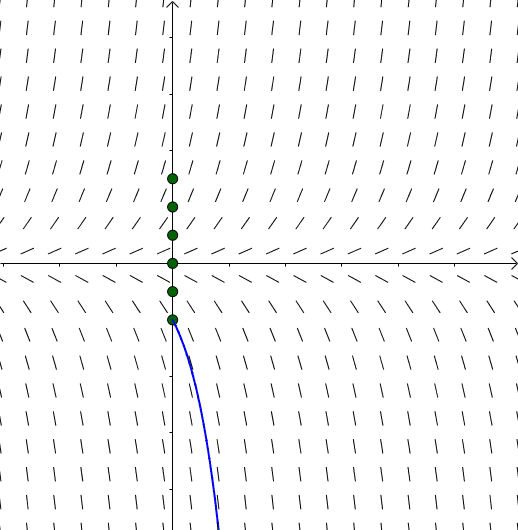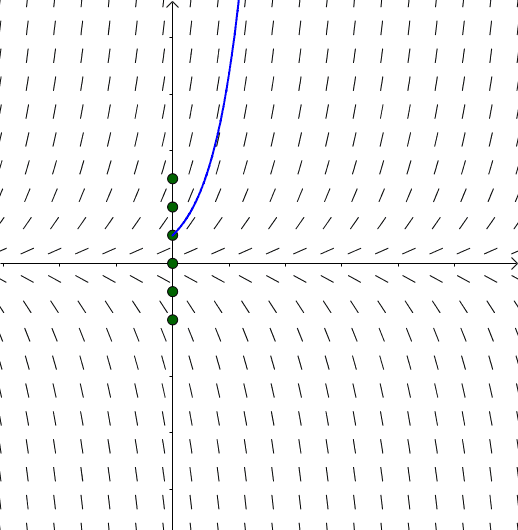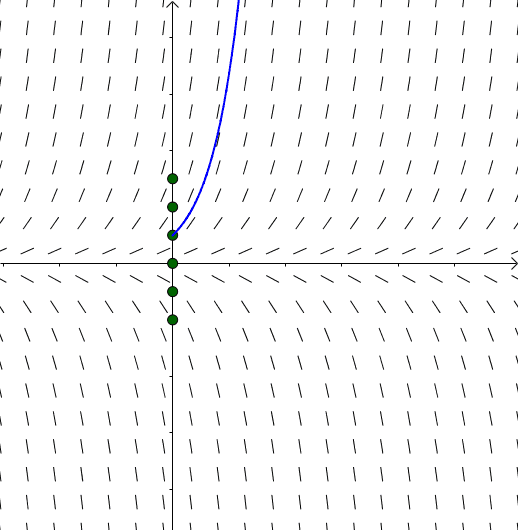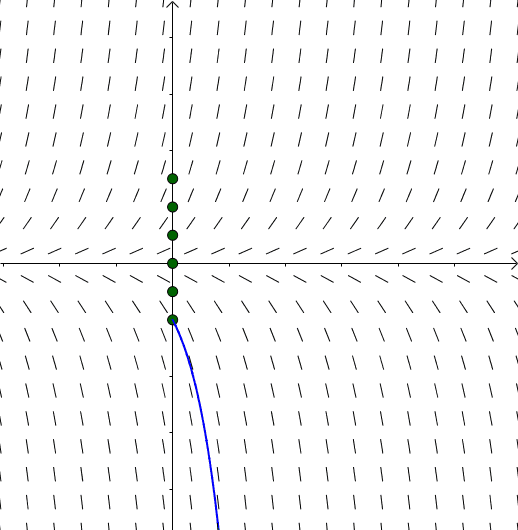
图12
不同的
，就相当于不同的初始值。不同的初始值得到的欧拉折线都是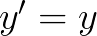
的一个特定的解（这里不用特解这个词，因为同济大学的书上的定义，特解是通解的一个特定解）。
这些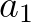
对应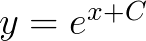
：
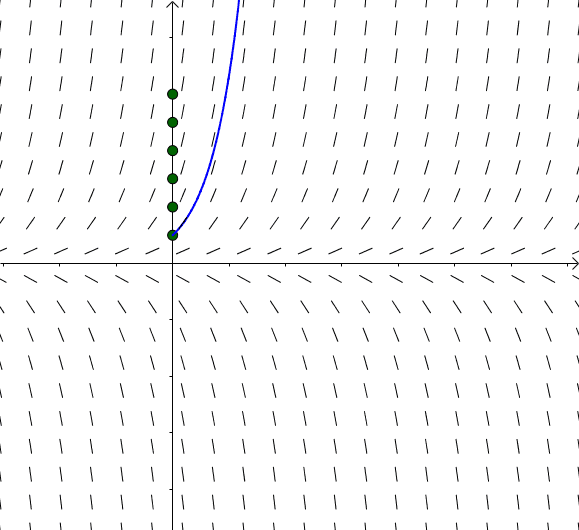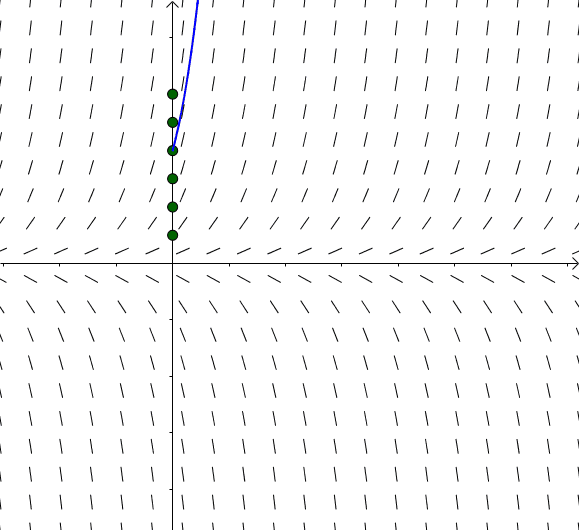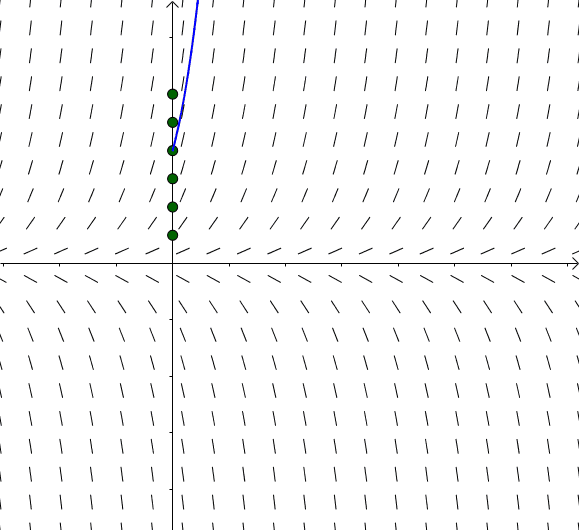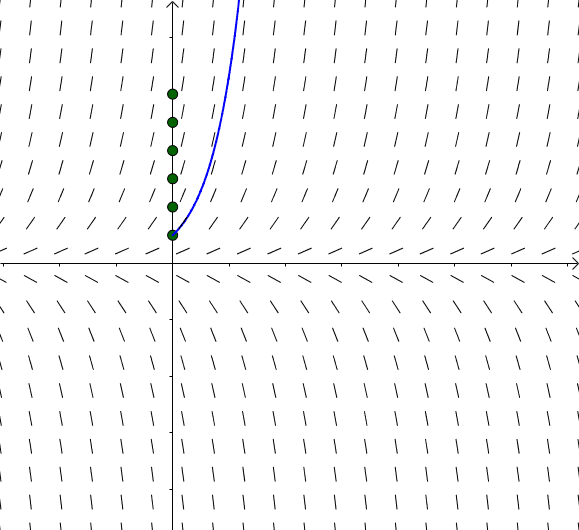
图13
这些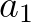对应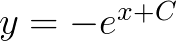
：
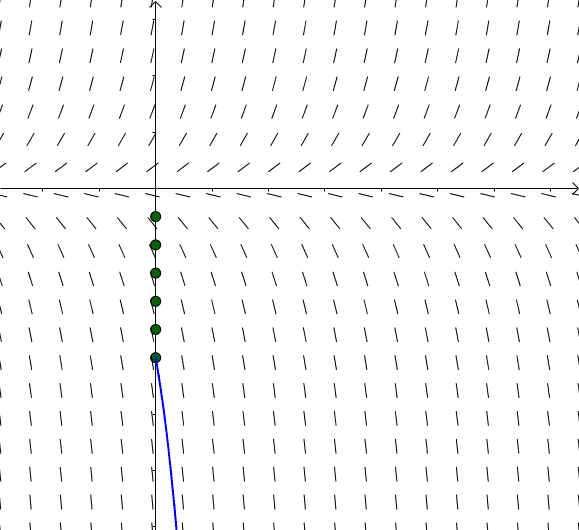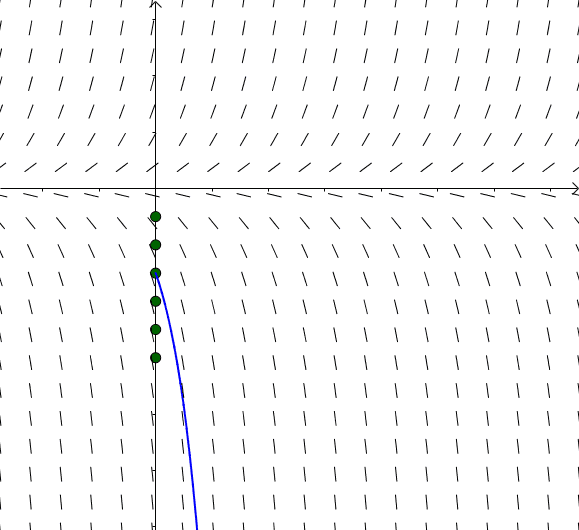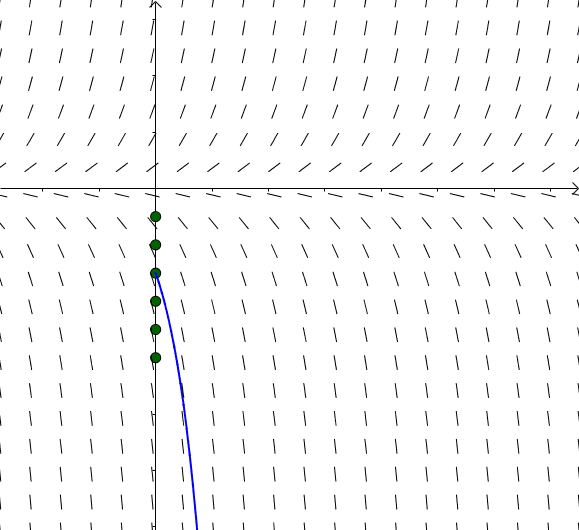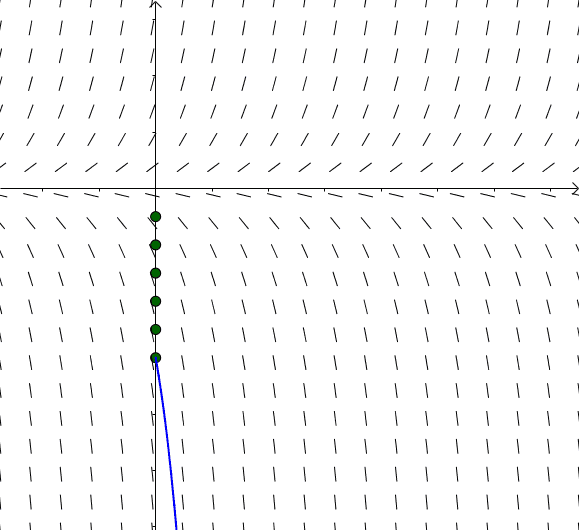
图14
容易观察到，还有一个解是通解里面没包含的，这就是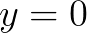
：
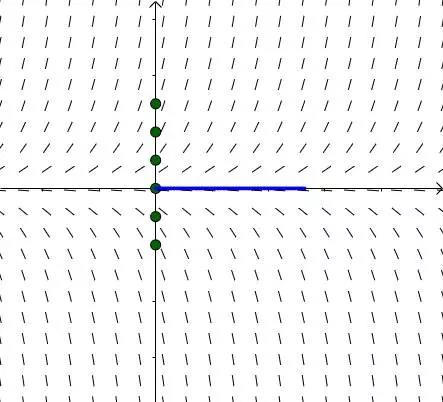
图15
你可以手动拖动下
，看看可以得到怎样的解：
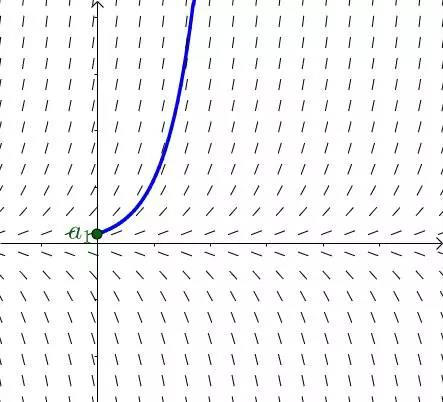
图16
此处有互动内容，点击最下面的“阅读原文”进行操作。
2. 小结
至此，我们可以得到以下结论：
微分方程往往有无数多个解
有一些解，可以写成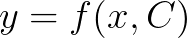
的形式，其中
为任意常数，称为通解
对于通解，特定的初始值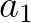
，可以得到一个特解
通解并不包含所有解
具体到刚才举的函数就是：
图17
五、一个小尾巴
有的同学说，如果我把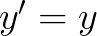
的通解写作：
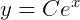
是不是通解就包含所有解的？
让我们来看看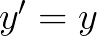
是如何求解的：
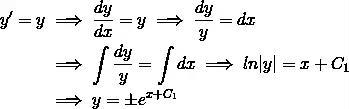
此时，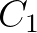
是任意常数。然后我们做个变形：
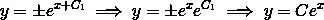
注意，此时的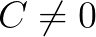
。
所以，按照书上的定义，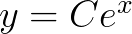
并不能称为通解。
当然，让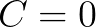
，正好可以得到
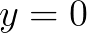这个解，实际上是一个巧合。
让我们另外举一个例子，就可以规避这种巧合：
图18
自己动手来试试这个微分方程（橙色曲线是某个特解，可以通过拖动条来改变；蓝色曲线是欧拉折线，可以拖动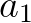
来改变）：
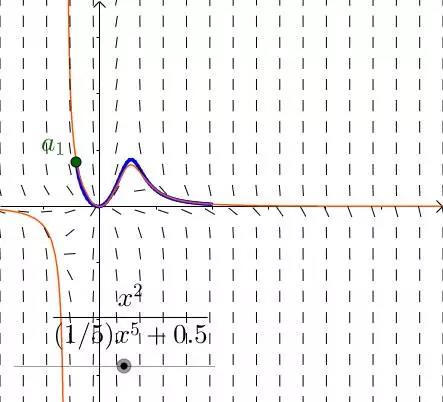
图19
此处有互动内容，点击最下面的“阅读原文”进行操作。
阅读原文
声明：文章转自【马同学高等数学】微信公众号，版权归原作者所有，转载仅供学习使用，不用于任何商业用途，如有侵权请联系删除，谢谢。
