在各种令人惊讶的数学事实当中,我最喜欢的类型之一便是,某个数学命题在二维空间、三维空间甚至四维空间当中都是成立的,但偏偏到了某个维度时,命题就不成立了。 Keller 猜想就是一个这样的例子。
同样大小的正方形平铺整个平面(比如像下图那样),则一定存在某些边与边完全贴合的相邻正方形。
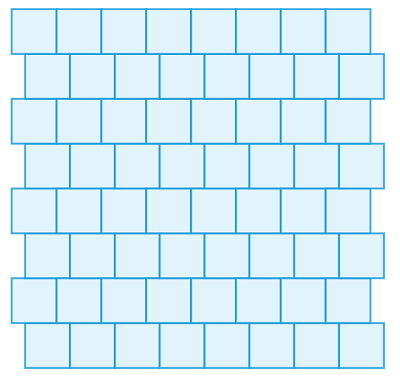
图1
类似地,同样大小的正方体平铺整个空间(比如像下图那样),则一定存在某些面与面完全贴合的相邻正方体。

图2
1930 年, Ott-Heinrich Keller 猜测,或许这一点对于更高维度的空间都是成立的。也就是说, Ott-Heinrich Keller 猜测,对于任意正整数 n ≥ 2 都有,同样大小的 n 维立方体平铺整个 n 维空间,则一定有两个面与面完全贴合的相邻 n 维立方体。这就是著名的 Keller 猜想。
1940 年, Oskar Perron 证明了,当 n = 2, 3, 4, 5, 6 时, Keller 猜想确实是正确的。一切似乎都在正轨上。然而,到了 1992 年的时候,事情出现了转折: Jeffrey Lagarias 和 Peter Shor 构造了一个 n = 12 时的反例,从而推翻了 Keller 猜想。让我们来看一看 Lagarias 和 Shor 的神构造吧。为了方便起见,下面我们直接用“立方体”一词指代 n 维的广义立方体,“立方体的面”则代表 n 维立方体的 n – 1 维面。
考虑所有只用 0 、 1 、 2 、 3 四个数组成的 n 维坐标,这样的坐标一共有 4n 个。现在,从中选择其中的 2n 个坐标,使得每两个坐标都有至少一个位置上的数相差正好为 2 。把这些坐标当作立方体的中心,作出一个个边长为 2 的立方体。容易看出,这些立方体将会满足:
● 任意两个立方体都不会有重合的部分;
● 即使这些立方体可以沿着各坐标轴方向 4 格 4 格地任意平移,任意两个立方体也仍然不会有重合的部分(本来相差 2 个单位的维度上仍然会差至少 2 个单位);
● 这些立方体的总体积是 2n · 2n = 4n ,正好等于一个边长为 4 的大立方体的体积。
因而,把这些立方体当作一个整体,沿着各坐标轴方向 4 格 4 格地平移,就能平铺整个空间了。不过,这样得到的平铺方案中,可能存在着完全贴合的相邻立方体。然而,如果我们选出的 2n 个坐标当中,每两个坐标之间不但有某个位置上的数正好相差 2 ,还有另外至少一个位置上的数也不同的话,那么相邻立方体就都是错开的了——即使平移之后,该错开的立方体仍然是错开的,因为 0 、 1 、 2 、 3 四个数当中的任意两个不同的数,不会因为它们各自加减了某些 4 的倍数而变得相同。
如果两个 n 维坐标满足,它们有至少一个维度上的坐标正好相差 2 ,而且还有至少一个维度上的坐标不同,我们就说这两个 n 维坐标是相容的。因此,为了构造出一个 n 维空间中 Keller 猜测的反例,我们只需要找出 2n 个由 0 、 1 、 2 、 3 四个数组成的 n 维坐标,使得里面的任意两个坐标都是相容的,
为了更好地说明上面这些话的意思,让我们来看一个 n = 3 时的例子。由 0 、 1 、 2 、 3 四个数组成的三维坐标一共有 43 = 64 个,我们选择以下 23 = 8 个:
● (0, 0, 0)
● (2, 0, 1)
● (1, 2, 0)
● (0, 1, 2)
● (2, 0, 3)
● (3, 2, 0)
● (0, 3, 2)
● (2, 2, 2)
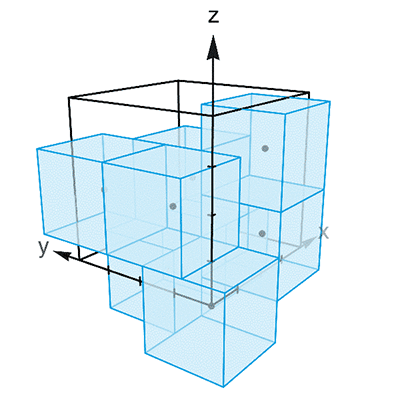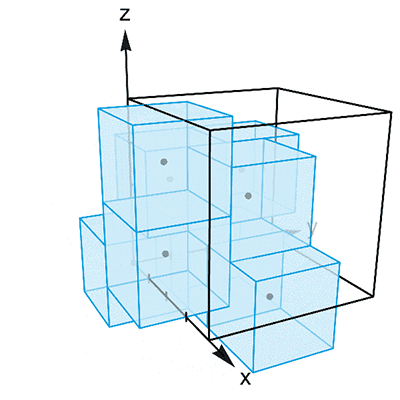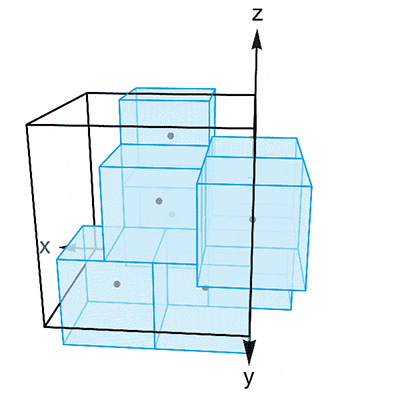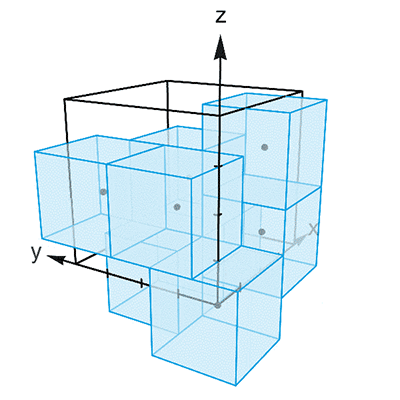
图3
注意到,上面这 8 个坐标中,每两个坐标都有至少一个位置上的数正好相差 2 。如果以它们为中心,作出一个个边长为 2 的立方体,你会发现不管从哪个方向上看,这些立方体排成的都是紧密的两层。因此,使用这种结构的组合体,就能平铺整个空间了。只可惜,在上面这 8 个坐标中, (2, 0, 1) 和 (2, 0, 3) 虽然有一个位置上正好相差 2 ,但在其他位置上的数都是相同的。因此,这两个坐标所对应的立方体就是完全贴合的。类似的情况还有 (1, 2, 0) 和 (3, 2, 0) ,以及 (0, 1, 2) 和 (0, 3, 2) 。因此,这 8 个坐标并不构成 n = 3 时 Keller 猜想的反例。不过, Lagarias 和 Shor 却以此为基础,成功构造出了 n = 12 时 Keller 猜想的反例。让我们暂时把 (2, 0, 3) 、 (3, 2, 0) 和 (0, 3, 2) 中的 0 替换成 0′ ,并且规定 0′ 和 0 是两个数值相等的不同元素。这样赖皮之后,这 8 个坐标暂时变得两两相容了:
● (0, 0, 0)
● (2, 0, 1)
● (1, 2, 0)
● (0, 1, 2)
● (2, 0′, 3)
● (3, 2, 0′)
● (0′, 3, 2)
● (2, 2, 2)
现在,我们要把它们变成 212 = 4096 个十二维坐标,使得所有坐标仍然是两两相容,并且里面不再有 0′ 这种东西。考虑 S0 、 S0′ 、 S1 、 S2 、 S3 这么五个集合,每个集合里面都有若干个四维坐标。这五个集合的具体情况如下:
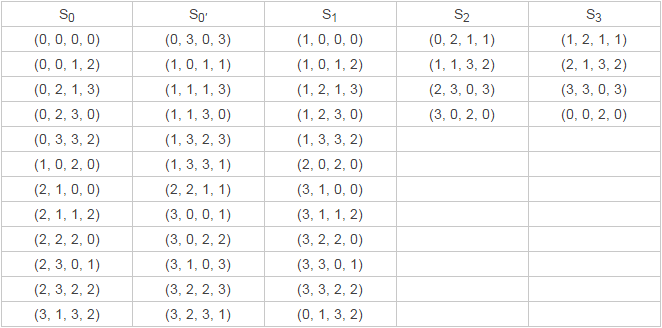
可以验证,这五个集合满足以下 5 个条件。
对于 S0 、 S0′ 、 S1 、 S2 、 S3 中的任意一个集合,里面的所有四维坐标都是两两相容的。
对于 S0 、 S0′ 、 S1 、 S2 、 S3 中的任意两个集合,里面都没有相同的四维坐标。
S0 中的每一个坐标和 S2 中的每一个坐标相比,都有一个位置上正好相差 2 。
S0′ 中的每一个坐标和 S2 中的每一个坐标相比,都有一个位置上正好相差 2 。
S1 中的每一个坐标和 S3 中的每一个坐标相比,都有一个位置上正好相差 2 。
这五个集合显然不是凭空构造出来的,绝大部分都是根据某些规律生成的。抓住这些规律,可以大大简化我们的验证工作。注意到, S1 可以看作是把 S0 里的每一个坐标的首位按照 {0 → 1, 1 → 2, 2 → 3, 3 → 0} 的规则进行替换后得来的, S3 也可以看作是对 S2 里的每一个坐标进行同样的变换后得来的。因此,如果 S0 中的坐标两两相容,则 S1 中的坐标也就两两相容了;如果 S2 中的坐标两两相容,则 S3 中的坐标也就两两相容了;还有,如果 S0 和 S2 满足条件 3 ,则 S1 和 S3 也一定满足条件 5 。另外, S0′ 又可以看作是把 S0 里的每一个坐标的首位按照 {0 → 1, 1 → 2, 2 → 3, 3 → 0} 的规则进行替换,再把末位按照 {0 → 3, 3 → 2, 2 → 1, 1 → 0} 的规则进行替换,最后把这两位交换之后得来的。因此,如果 S0 中的坐标两两相容,则 S0′ 中的坐标也就两两相容了。有趣的是,对 S2 里的所有坐标进行同样的变换后,得到的集合正好是它自己。因此, S0 和 S2 一旦满足条件 3,则 S0′ 和 S2 也就自动地满足条件 4 了。最终,我们真正需要验证的就只有条件 2 和条件 3 ,以及条件 1 中的 S0 和 S2 这两个集合。如果你感兴趣的话,不妨自己验证一下。
还记得刚才那 8 个赖皮之后暂时变得两两相容的三维坐标吗?现在,从中任取一个坐标,将各个位置上的数都替换成对应集合里的某个四维坐标,我们就能够得到各种各样的十二维坐标了。例如, S2 里面有 4 个四维坐标, S0′ 里面有 12 个四维坐标, S3 里面有 4 个四维坐标,因此从 (2, 0′, 3) 出发,一共就可以派生出 4 × 12 × 4 = 192 个十二维坐标。照这样做下去,我们一共能派生出多少个十二维坐标呢?让我们来算一算。
(0, 0, 0) → 12 × 12 × 12 = 1728
(2, 0, 1) → 4 × 12 × 12 = 576
(1, 2, 0) → 12 × 4 × 12 = 576
(0, 1, 2) → 12 × 12 × 4 = 576
(2, 0′, 3) → 4 × 12 × 4 = 192
(3, 2, 0′) → 4 × 4 × 12 = 192
(0′, 3, 2) → 12 × 4 × 4 = 192
(2, 2, 2) → 4 × 4 × 4 = 64
总计: 1728 + 576 × 3 + 192 × 3 + 64 = 4096
这正好等于 212 。下面我们证明,这 212 个十二维坐标是两两相容的。
容易看出,对于任意一个三维坐标来说,由它派生出来的各个十二维坐标互相之间肯定是两两相容的。这是因为,如果两个不同的十二维坐标是由同一个三维坐标派生出来的,这就说明它们的前段、中段、后段分别取材于同样的三个集合,并且至少有一段取得有所不同;条件 1 保证了单看这一段的话两者是相容的,根据相容性的定义,整个十二维坐标也就是相容的了。
那么,两个不同的三维坐标所派生的十二维坐标,为什么也一定是相容的呢?首先,两个不同的三维坐标当中,肯定有某一个位置上的数相差为 2 ,由条件 3 到 5 可知,这一点会被继承下去;另外,这两个三维坐标当中肯定还有另外一个位置上有不同的元素,由条件 2 可知,这一点会被继承下去。至此,我们就得到了 n = 12 时 Keller 猜想的一个完整的反例。
显然,低维空间中的任何反例,都可以立即变成高维空间中的反例,我们只需要把低维空间中的反例一层一层地搭起来,每一层都和前一层错开一点即可。因此, n = 12 时的 Keller 猜想被推翻了,则 n ≥ 12 时的 Keller 猜想也就全被推翻了。
在同一篇论文中, Jeffrey Lagarias 和 Peter Shor 紧接着构造出了 n = 10 时 Keller 猜想的反例,背后的思想基本相同。 2002 年, John Mackey 给出了一个 n = 8 时的反例。这说明, n ≥ 8 时的 Keller 猜想全是错的。至此, Keller 猜想只剩下了一个遗留问题:当 n = 7 时, Keller 猜想是否成立。这个问题至今仍未解决。
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











