y = x2 似乎把 y = x 远远地甩在了后面,但为何当 x 无穷大时,二者能同时到达无穷?当 x 从有限大变为无限大时, 1 / x 的函数值是怎样慢慢变成 0 的? y = ex, y = xx, y = x! ,谁的函数值最先接近无穷? y = ln x, y = x · ln x, y = √x ,谁的函数值最后接近无穷?下面这个有趣的方法能直观地展示出函数图象在无穷远处的样子,进而回答刚才这些看似毫无意义的问题。
当 x 从 -π/2 连续地增加到 π/2 时, x 的正切值将会从负无穷连续地增加到正无穷。因此,为了展示出 y = f(x) 在无穷远处的样子,我们可以画出 tan(y) = f(tan(x)) 在 (-π/2, π/2) × (-π/2, π/2) 上的图象,也就是 y = arctan(f(tan(x))) 在 (-π/2, π/2) × (-π/2, π/2) 上的图象。最后得到的结果是什么样的呢?让我们一起来看看吧。
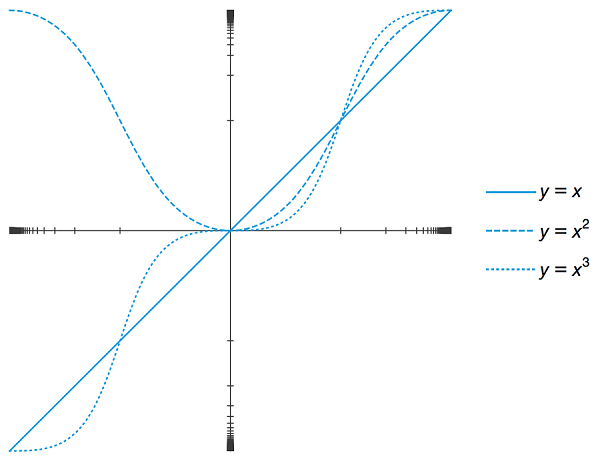
图1
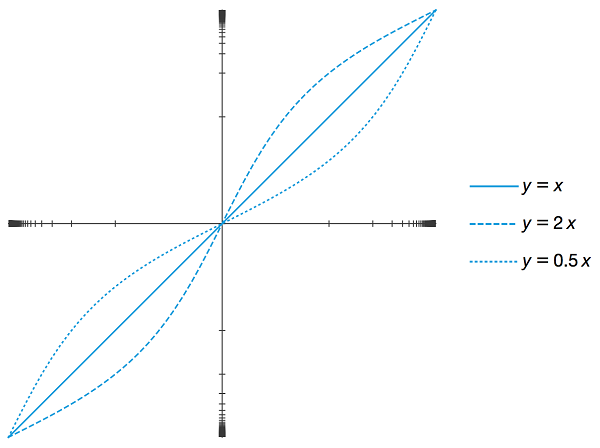
图2
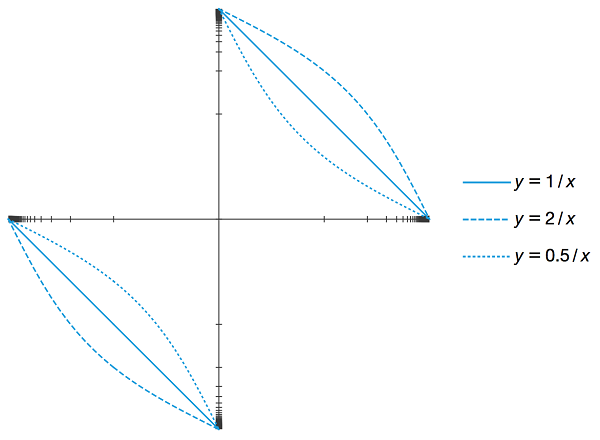
图3
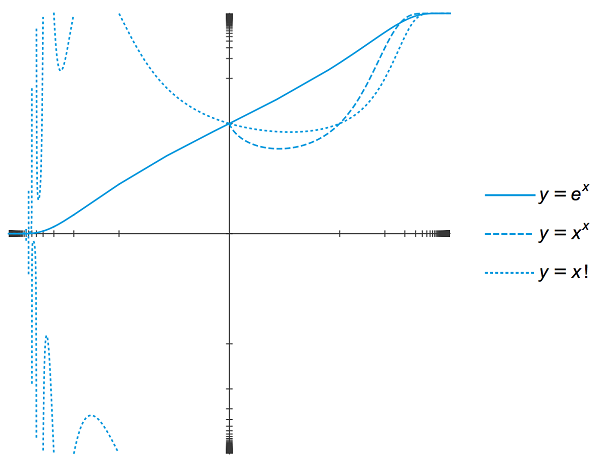
图4
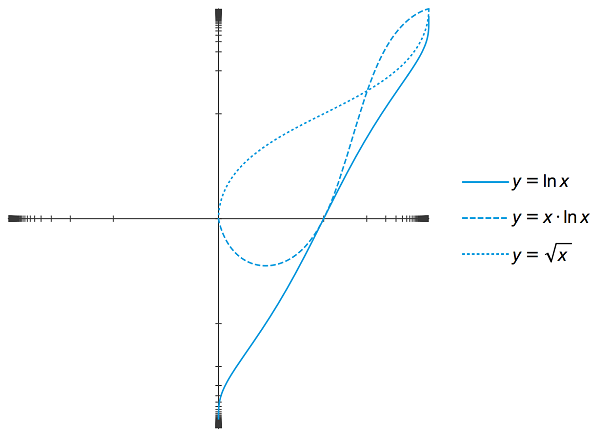
图5
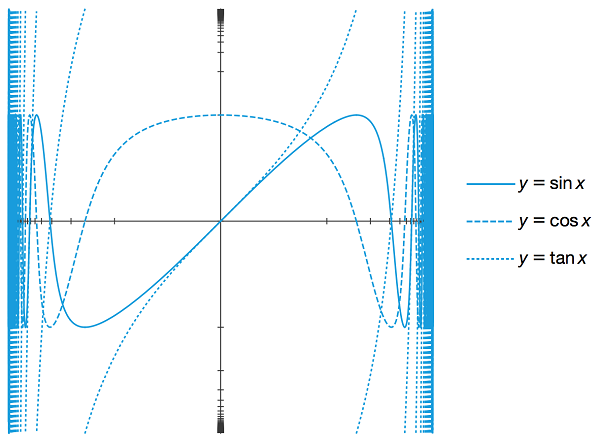
图6
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











