先把问题完整的描述下。
如果已知随机变量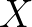
的期望为
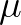，那么可以如下计算方差
：
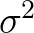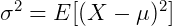
上面的式子需要知道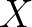
的具体分布是什么（在现实应用中往往不知道准确分布），计算起来也比较复杂。
所以实践中常常采样之后，用下面这个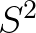
来近似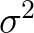
：
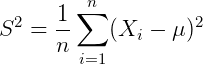
其实现实中，往往连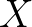
的期望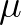
也不清楚，只知道样本的均值：
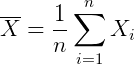
那么可以这么来计算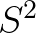
：
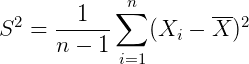
那这里就有两个问题了：
为什么可以用
来近似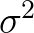
？
为什么使用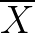
替代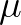
之后，分母是
？
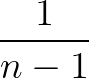我们来仔细分析下细节，就可以弄清楚这两个问题。
1. 为什么可以用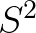
来近似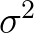
？
举个例子，假设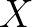
服从这么一个正态分布：
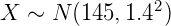
即，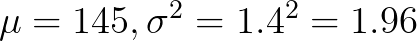
，图形如下：
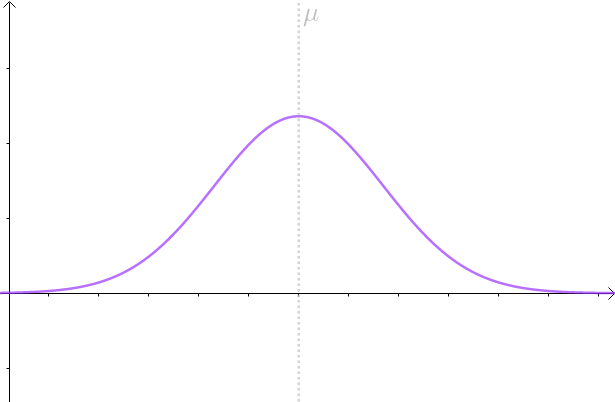
图1
当然，现实中往往并不清楚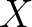
服从的分布是什么，具体参数又是什么？所以我用虚线来表明我们并不是真正知道
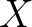的分布：
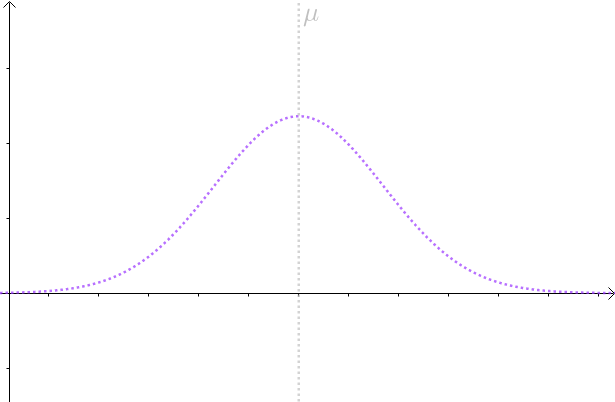
图2
很幸运的，我们知道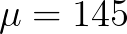
，因此对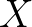
采样，并通过：
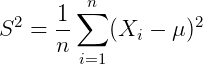
来估计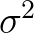
。某次采样计算出来的
：
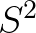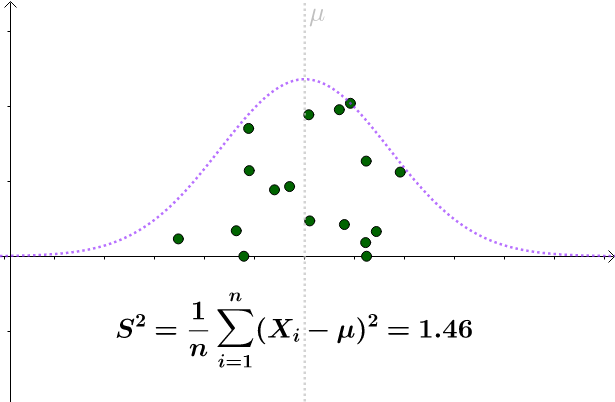
图3
看起来比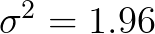
要小。采样具有随机性，我们多采样几次，
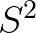会围绕
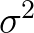上下波动：
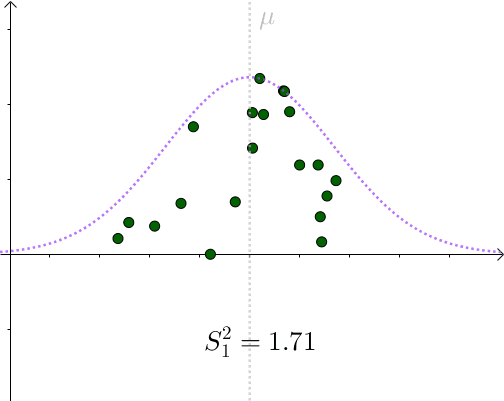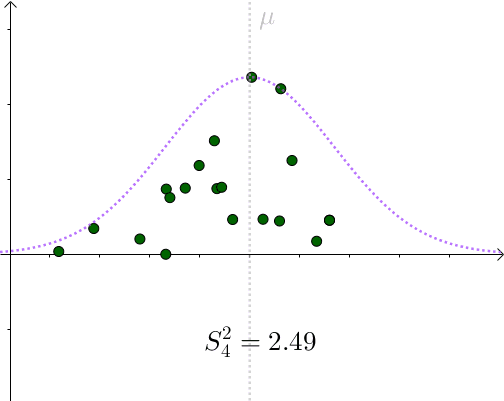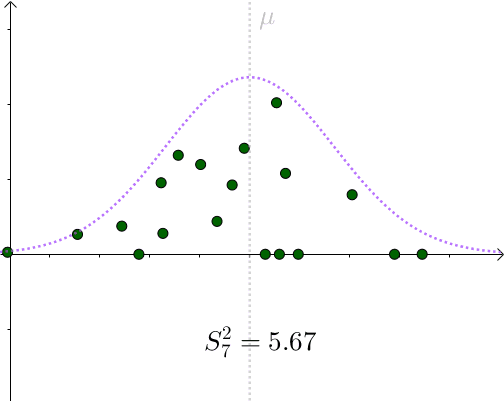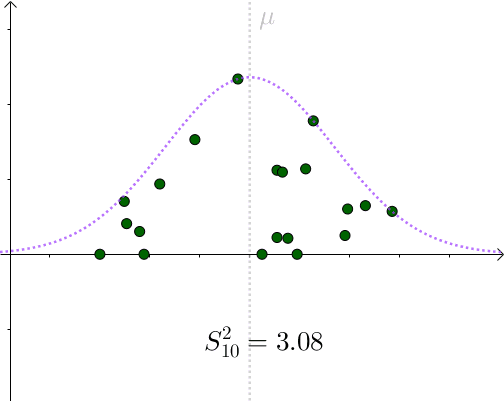
图4
用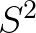
作为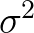
的一个估计量，算是可以接受的选择。
很容易算出：
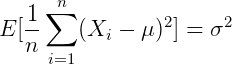
因此，根据中心极限定理，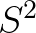
的采样均值会服从
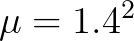的正态分布：
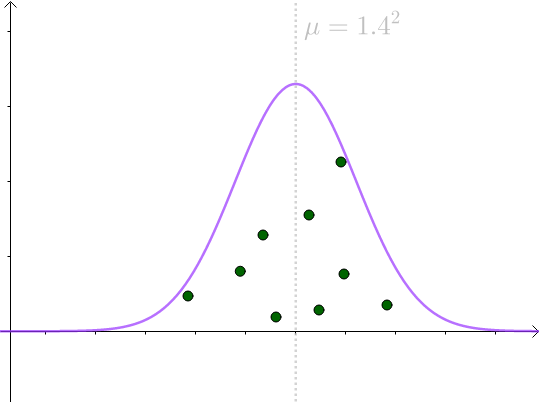
图5
这也就是所谓的无偏估计量。从这个分布来看，选择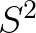
作为估计量确实可以接受。
2. 为什么使用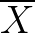
替代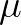
之后，分母是
？
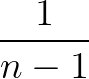更多的情况，我们不知道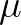
是多少的，只能计算出
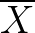。不同的采样对应不同的
：
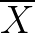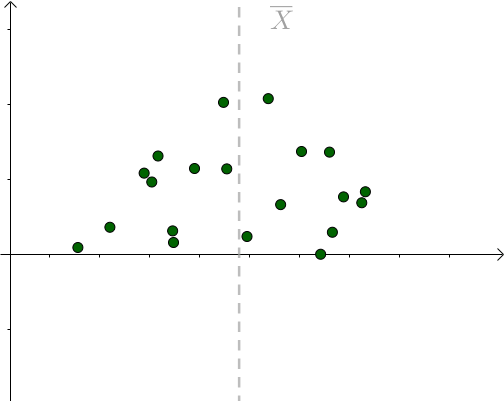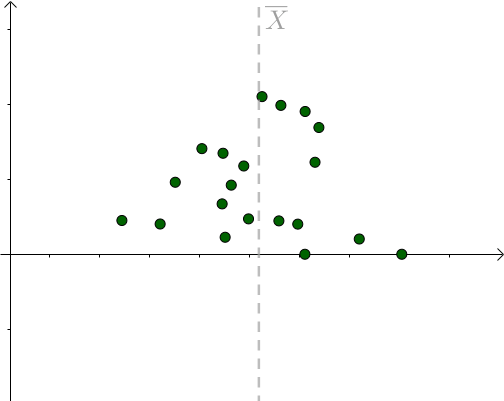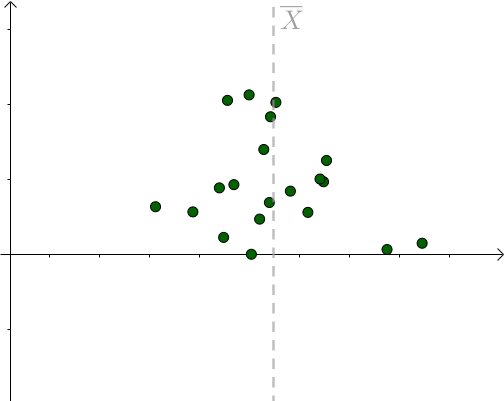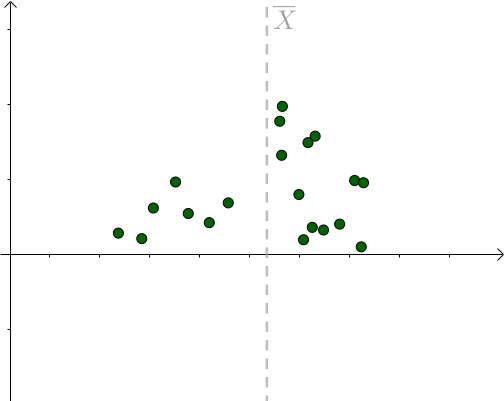
图6
对于某次采样而言，当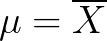
时，下式取得最小值：
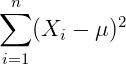
我们也是比较容易从图像中观察出这一点，只要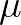
偏离
，该值就会增大：
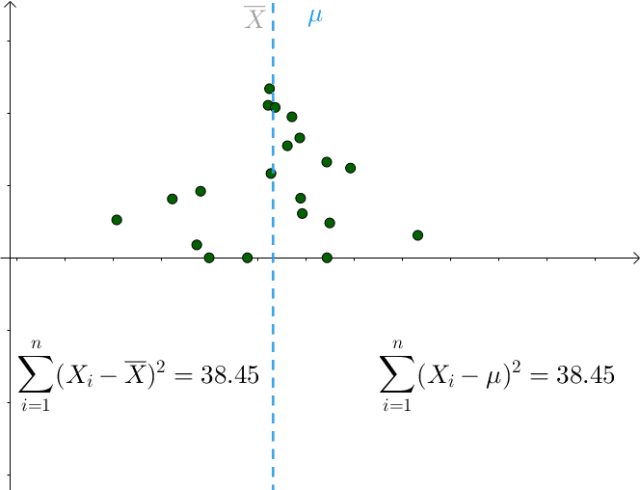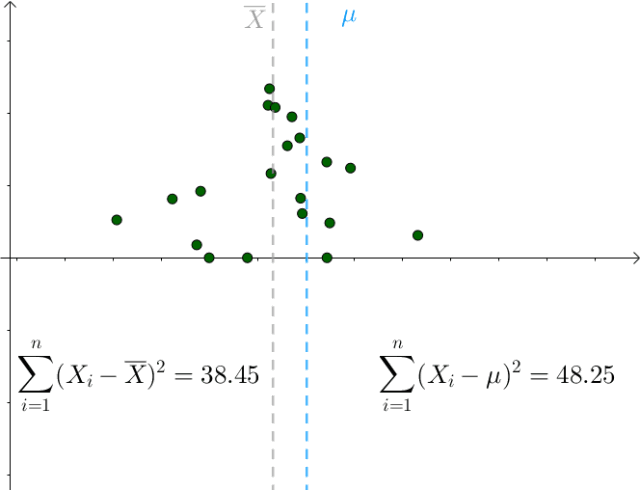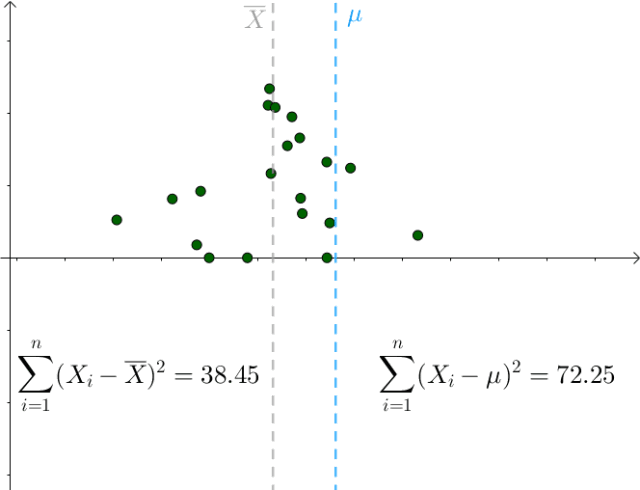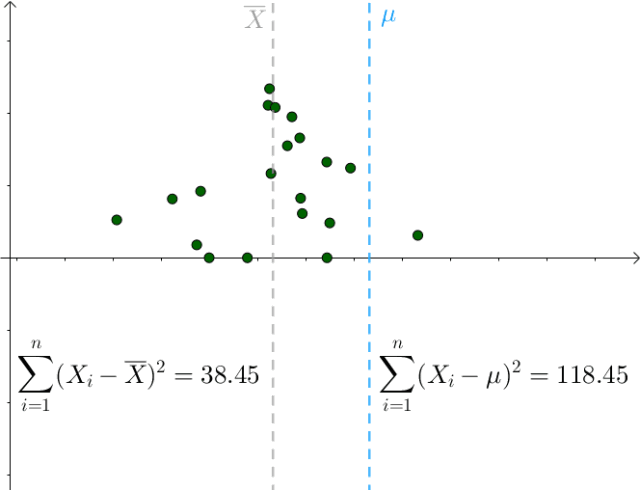
图7
所以可知：
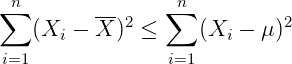
可推出：
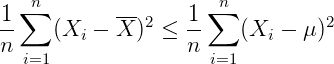
进而推出：
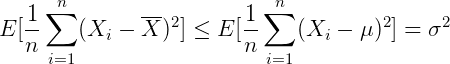
如果用下面这个式子来估计：
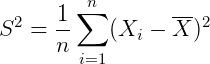
那么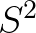
采样均值会服从一个偏离
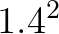的正态分布：
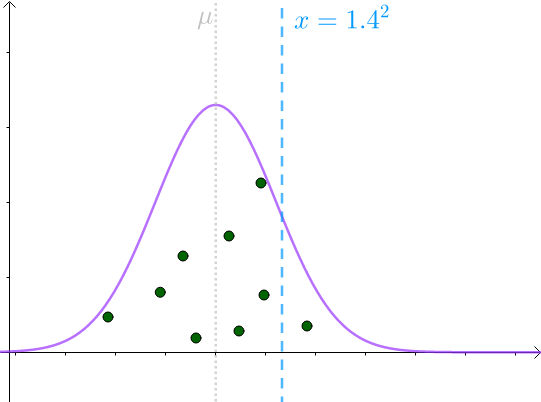
图8
可见，此分布倾向于低估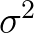
。
具体小了多少，我们可以来算下：
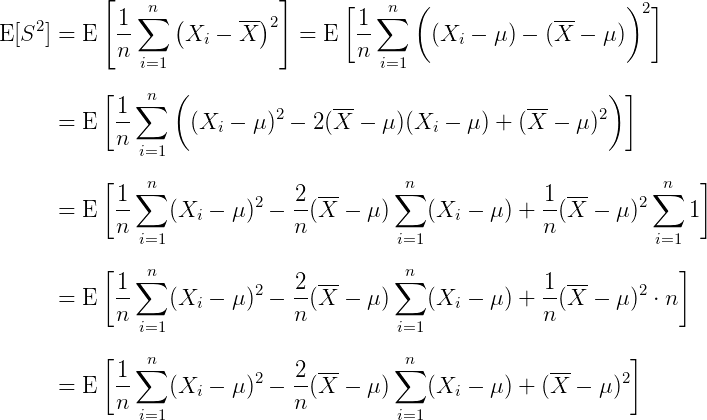
其中：
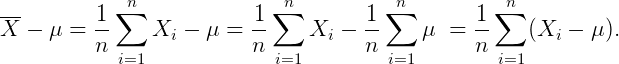
所以我们接着算下去：
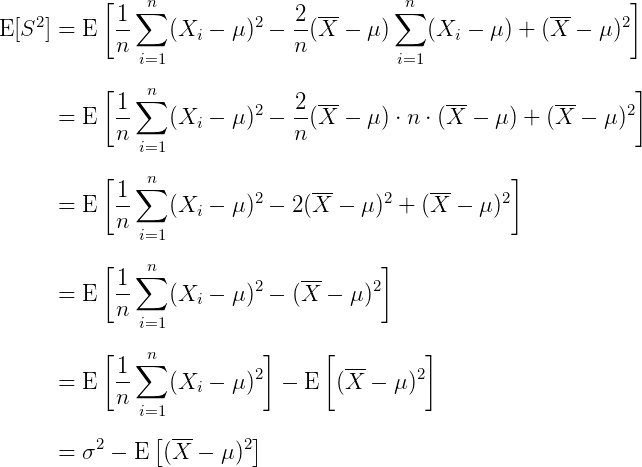
其中（证明见此）：
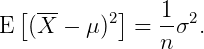
所以：
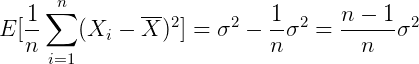
也就是说，低估了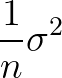
，进行一下调整：
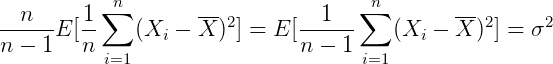
因此使用下面这个式子进行估计，得到的就是无偏估计：
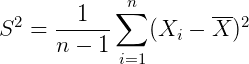
声明：文章转自【马同学高等数学】微信公众号，版权归原作者所有，转载仅供学习使用，不用于任何商业用途，如有侵权请联系删除，谢谢。
