国外有人发现一个鲜为人知的古董级函数作图软件—— GrafEq 。这个软件只有 2M 大小,它的功能就只有一个:作出形如 x2 + y2 = 1 的二元等式或者不等式的图像。令人惊叹的是,这个软件的图像绘制能力异常强大, Mathematica 等大型专业数学软件完全不是它的对手。
这个软件早就没再更新了。它的“最新版本”是 2.12 ,只支持 Windows 95 到 Windows XP 的系统,或者 PowerPC 7.12 到 MacOS 9.2 的系统,可见其年代久远。神奇的是,这个软件的官方网站依然健在,而且软件竟然也都能下载。如果你有幸还能装上这款软件,你将有机会重温一次 Windows 95 时代的软件安装画面。
一些带有三角函数的方程,某些地方的图像变化非常剧烈,连 Mathematica 也无法准确地描绘出来:
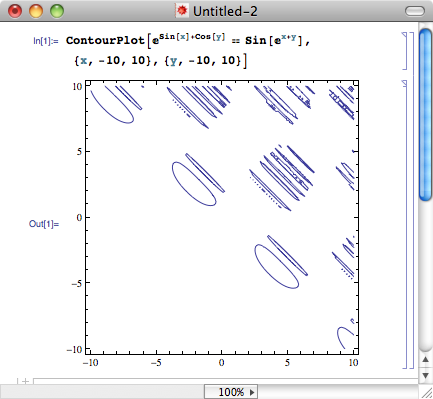
图1
然而, GrafEq 却能很好地描绘出来:

图2
注意,方程的图像显然无法形成实心的方块,这只是因为图像太密集罢了。
既然有机会见到各种方程图像的真容,我们当然要多尝试一些更复杂的方程。下面是另外几个例子:

图3

图4

图5
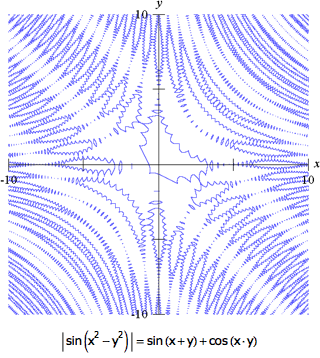
图6
要比哪个图像最帅,还是要数 GrafEq 官方网站上提供的一个示例:

图7
2011-10-07 Update: 今天,我碰巧看到了这个软件的来头(事实上,本页 29 楼的网友 zhangyoufu 也提到了)。这个软件的算法是 Jeff Tupper 在 2001 年的一篇论文中提出的,感兴趣的读者可以在这里看到: http://www.dgp.toronto.edu/people/mooncake/papers/SIGGRAPH2001_Tupper.pdf
在这篇论文中, Jeff Tupper 创作了很多漂亮的函数图像,其中一个就是著名的 Tupper 自我指涉公式 。论文中还有几个精彩的图像,我也重新绘制了一遍,贴出来和大家一同分享。

图8
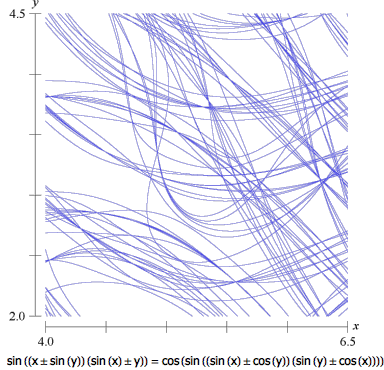
图9

图10
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











