谬证大全：1+1≠2的n种可能

最近看到几个有趣的数学谬证，想写下来与大家分享；结果写到这个又想到那个，一写就写个没完，于是想到干脆做一篇谬证大全，收集各种荒谬的证明。如果你有什么更棒的“证明”，欢迎来信与我分享，我会更新到这篇日志中。我的邮箱是 matrix67 at tom.com ，或者 gs.matrix67 at gmail.com 。

一、1=2？史上最经典的“证明”

设 a = b ，则 a·b = a² ，等号两边同时减去 b² 就有 a·b – b² = a² – b² 。注意，这个等式的左边可以提出一个 b ，右边是一个平方差，于是有 b·(a – b) = (a + b)(a – b) 。约掉 (a – b) 有 b = a + b 。然而 a = b ，因此 b = b + b ，也即 b = 2b 。约掉 b ，得 1 = 2 。

这可能是有史以来最经典的谬证了。 Ted Chiang 在他的短篇科幻小说 Division by Zero 中写到：There is a well-known “proof” that demonstrates that one equals two. It begins with some definitions: “Let a = 1; let b = 1.” It ends with the conclusion “a = 2a,” that is, one equals two. Hidden inconspicuously in the middle is a division by zero, and at that point the proof has stepped off the brink, making all rules null and void. Permitting division by zero allows one to prove not only that one and two are equal, but that any two numbers at all—real or imaginary, rational or irrational—are equal.

这个证明的问题所在想必大家都已经很清楚了：等号两边是不能同时除以 a – b 的，因为我们假设了 a = b ，也就是说 a – b 是等于 0 的。

二、无穷级数的力量
 

无穷级数的力量 (1)

小学时，这个问题困扰了我很久：下面这个式子等于多少？1 + (-1) + 1 + (-1) + 1 + (-1) + …
一方面，
1 + (-1) + 1 + (-1) + 1 + (-1) + …
= [1 + (-1)] + [1 + (-1)] + [1 + (-1)] + …
= 0 + 0 + 0 + …
= 0

另一方面，
1 + (-1) + 1 + (-1) + 1 + (-1) + …
= 1 + [(-1) + 1] + [(-1) + 1] + [(-1) + …
= 1 + 0 + 0 + 0 + …
= 1
这岂不是说明 0 = 1 吗？

后来我又知道了，这个式子还可以等于 1/2 。不妨设 S = 1 + (-1) + 1 + (-1) + … ， 于是有 S = 1 – S ，解得 S = 1/2 。

学习了微积分之后，我终于明白了，这个无穷级数是发散的，它没有一个所谓的“和”。无穷个数相加的结果是多少，这个是需要定义的。

无穷级数的力量 (2)

同样的戏法可以变出更多不可思议的东西。例如，令
x = 1 + 2 + 4 + 8 + 16 + …
则有
2x = 2 + 4 + 8 + 16 + …
于是
2x – x = x = (2 + 4 + 8 + 16 + …) – (1 + 2 + 4 + 8 + 16 + …) = -1
也就是说
1 + 2 + 4 + 8 + 16 + … = -1

三、平方根的阴谋
 

平方根的阴谋 (1)

定理：所有数都相等。
证明：取任意两个数 a 和 b ，令 t = a + b 。于是，
a + b = t
(a + b)(a – b) = t(a – b)
a² – b² = t·a – t·b
a² – t·a = b² – t·b
a² – t·a + (t²)/4 = b² – t·b + (t²)/4
(a – t/2)² = (b – t/2)²
a – t/2 = b – t/2
a = b

怎么回事儿？问题出在倒数第二行。永远记住， x² = y² 并不能推出 x = y ，只能推出 x = ±y 。

平方根的阴谋 (2)
1 = √1 = √(-1)(-1) = √-1·√-1 = -1

嗯？只有 x 、 y 都是正数时， √x·y = √x·√y 才是成立的。-1 的平方根有两个， i 和 -i 。 √(-1)(-1) 展开后应该写作 i·(-i) ，它正好等于 1 。

四、复数才是王道

考虑方程
x² + x + 1 = 0
移项有
x² = – x – 1
等式两边同时除以 x ，有
x = – 1 – 1/x
把上式代入原式中，有
x² + (-1 – 1/x) + 1 = 0
即
x² – 1/x = 0
即
x³ = 1
也就是说 x = 1。
把 x = 1 代回原式，得到 1² + 1 + 1 = 0 。也就是说， 3 = 0 ，嘿嘿！

其实， x = 1 并不是方程 x² + x + 1 = 0 的解。在实数范围内，方程 x² + x + 1 = 0 是没有解的，但在复数范围内有两个解。

另一方面， x = 1 只是 x³ = 1 的其中一个解。 x³ = 1 其实一共有三个解，只不过另外两个解是复数范围内的。考虑方程 x³ – 1 = (x – 1)(x² + x + 1) = 0 ，容易看出 x³ = 1 的两个复数解正好就是 x² + x + 1 的两个解。因此， x² + x + 1 = 0 与 x³ = 1 同时成立并无矛盾。

注意，一旦引入复数后，这个谬论才有了一个完整而漂亮的解释。或许这也说明了引入复数概念的必要性吧。

五、颇具喜剧色彩的错误

众所周知，
1 + 2 + 3 + … + n = n(n+1) / 2
让我们用 n – 1 去替换 n ，可得
1 + 2 + 3 + … + (n-1) = (n-1)n / 2
等式两边同时加 1 ，得：
1 + 2 + 3 + … + n = (n-1)n / 2 + 1
也就是
n(n+1) / 2 = (n-1)n / 2 + 1
展开后有
n² / 2 + n / 2 = n² / 2 – n / 2 + 1
可以看到 n = 1 是这个方程的唯一解。

也就是说⋯⋯ 1 + 2 + 3 + … + n = n(n+1) / 2 仅在 n = 1 时才成立！

这个推理过程中出现了一个非常隐蔽而搞笑的错误。等式两边同时加 1 后，等式左边得到的应该是1 + 2 + 3 + … + (n-2) + (n-1) + 1

六、1 块钱等于 1 分钱？

我要用数学的力量掏空你的钱包！请看：1 元 = 100 分 = (10 分)² = (0.1 元)² = 0.01 元 = 1 分

用这个来骗小孩子们简直是屡试不爽，因为小学（甚至中学）教育忽视了一个很重要的思想：单位也是要参与运算的。事实上， “100 分 = (10 分)²” 是不成立的， “10 分” 的平方应该是 “100 平方分” ，正如 “10 米” 的平方是 “100 平方米” 一样。

七、数学归纳法的杯具

数学归纳法的杯具 (1)

下面这个“证明”是由数学家 George Pólya 给出的：任意给定 n 匹马，可以证明这 n 匹马的颜色都相同。

对 n 施归纳：首先，当 n = 1 时命题显然成立。若命题对 n = k 成立，则考虑 n = k + 1 的情形：由于 {#1, #2, …, #k} 这 k 匹马的颜色相同， {#2, #3, …, #k+1 } 这 k 匹马也相同，而这两组马是有重叠的，可知这 k+1 匹马的颜色也都相同了。

这个证明错在，从 n = 1 推不出 n = 2 ，虽然当 n 更大的时候，这个归纳是正确的。这是数学归纳法出错的一个比较奇特的例子：基础情形和归纳推理都没啥问题，偏偏卡在归纳过程中的某一步上。

数学归纳法的杯具 (2)

下面，我来给大家证明，所有正整数都相等。

为了证明这一点，只需要说明对于任意两个正整数 a 、 b ，都有 a = b 。

为了证明这一点，只需要说明对于所有正整数 n ，如果 max(a, b) = n ，那么 a = b 。

我们对 n 施归纳。当 n = 1 时，由于 a 、 b 都是正整数，因此 a 、 b 必须都等于 1 ，所以说 a = b 。若当 n = k 时命题也成立，现在假设 max(a, b) = k + 1 。则 max(a – 1, b – 1) = k ，由归纳假设知 a – 1 = b – 1 ，即 a = b 。

这个问题出在， a – 1 或者 b – 1 有可能不是正整数了，因此不能套用归纳假设。

八、1 是最大的正整数？

来自网友 boring David 发来的邮件。

证明： 1 是最大的正整数。假设最大的正整数不是 1 ，是 a ，则必有 a > 1 。于是有 a² > a ，即 a² 是一个比 a 更大的正整数，与 a 的最大性矛盾。因此 1 是最大的正整数。

这个证明是错误的。在假设最大正整数是 a 之前，你得先说明它的存在性，排除最大的正整数根本不存在的可能性（而事实情况正是后者）。

九、所有三角形都是等腰三角形

别以为谬证都是隐藏在数字和字母之中的。下面就是一个经典的几何谬论。

画一个任意三角形 ABC 。下面我将证明， AB = AC ，从而说明所有三角形都是等腰三角形。

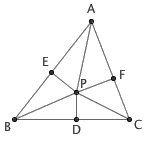
图1

令 BC 的中垂线与 ∠A 的角平分线交于点 P 。过 P 作 AB 、 AC 的垂线，垂足分别是 E 、 F 。由于 AP 是角平分线，因此 P 到两边的距离相等，即 PE = PF 。于是，由 AAS 可知 △APE ≌ △APF 。由于 DP 是中垂线，因此 P 到 B 、 C 的距离相等，由 SSS 可知 △BPD ≌ △CPD 。另外，由于 PE = PF ， PB = PC ，且 ∠BEP = ∠CFP = 90° ，由 HL 可知 △BEP ≌ △CFP 。现在，由第一对全等三角形知 AE = AF ，由最后一对全等三角形知 BE = CF ，因此 AE + BE = AF + CF ，即 AB = AC 。

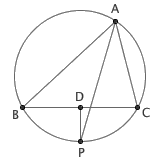
图2

这个证明过程其实字字据理，并无破绽。证明的问题出在一个你完全没有意识到的地方——这个图形就是错的！事实上， BC 的中垂线与 ∠A 的角平分线不可能交于三角形的内部。我们可以证明， P 点总是落在 △ABC 的外接圆上。如图， P 是 BC 的中垂线与外接圆的交点，显然 P 就是弧 BC 的中点，即弧 BP = 弧 PC 。因此， ∠BAP = ∠CAP ，换句话说 P 恰好就在 ∠A 的角平分线上。

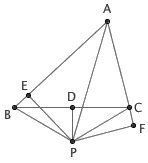
图3

P 在 △ABC 外的话，会对我们的证明产生什么影响呢？你会发现，垂足的位置发生了本质上的变化—— F 跑到 AC 外面去了！也就是说，结论 AE + BE = AF + CF 并不错，只是 AF + CF 并不等于 AC 罢了。

十、一个可怕的逻辑错误

下面这个勾股定理的“证明”曾经发表在 1896 年的 The American Mathematical Monthly 杂志上：

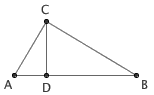
图4

假设勾股定理是正确的，于是我们可以得到
AB² = AC² + BC²
BC² = CD² + BD²
AC² = AD² + CD²
把后两式代入第一个式子，有
AB² = AD² + 2·CD² + BD²
但 CD² = AD·BD ，因此
AB² = AD² + 2·AD·BD + BD²
即
AB² = (AD + BD)²
即
AB = AD + BD
而这显然成立。因此，我们的假设也是成立的。

这个证明是错误的。假设结论正确，推出一个矛盾，确实能说明这个假设是错误的（这就是反证法）；但假设结论正确，推出它与条件吻合，这却并不能说明假设真的就是正确的。错误的假设也有可能推出正确的结果来。最经典的例子就是，不妨假设 1 = 2 ，由等式的对称性可知 2 = 1 ，等量加等量有 1+2 = 2+1 ，即 3 = 3 。但 3 = 3 是对的并不能表明 1 = 2 是对的。

十一、如此反证

下面这个有趣的故事来源于 Lewis Carroll 的一篇题为 A Logical Paradox 的小论文。

Joe 去理发店理发。理发店有 A 、 B 、 C 三位师傅，但他们并不总是待在理发店里。 Joe 最喜欢 C 的手艺，他希望此时 C 在理发店里。他远远地看见理发店还开着，说明里面至少有一位师傅。另外， A 是一个胆小鬼，没有 B 陪着的话 A 从不离开理发店。
Joe 推出了这么一个结论： C 必然在理发店内。让我们来看看他的推理过程。

反证，假设 C 不在理发店。这样的话，如果 A 也不在理发店，那么 B 就必须在店里了，因为店里至少有一个人；然而，如果 A 不在理发店， B 也理应不在理发店，因为没有 B 陪着的话 A 是不会离开理发店的。因此，由 “C 不在理发店” 同时推出了 “若 A 不在则 B 一定在” 和 “若 A 不在则 B 也一定不在” 两个矛盾的结论。这说明， “C 不在理发店” 的假设是错误的。

从已有的条件看， C 当然有可能不在理发店。但是，为什么 Joe 竟然证出了 C 一定在理发店呢？因为他的证明是错的。其实， “若 A 不在则 B 一定在” 和 “若 A 不在则 B 也一定不在” 并不矛盾——如果事实上 A 在理发店，那么这两个条件判断句都是真的。 “若 A 不在则 B 一定在” 真正的否定形式应该是 “A 不在并且 B 也不在” 。

十二、自然语言的表达能力

我曾在另类搞笑：自我指涉例句不完全收集一文中写过。

定理：所有的数都可以用 20 个以内的汉字表达（比如 25852016738884976640000 可以表达为“二十三的阶乘”， 100000000000000000000000 可以表达为“一后面二十三个零”）

证明：反证，假设存在不能用 20 个以内的汉字表达的数，则必有一个最小的不能用 20 个以内的汉字表达的数，而这个数已经用“最小的不能用 20 个以内的汉字表达的数”表达出来了，矛盾。

当然，这个定理明显是错的，因为 20 个汉字的组合是有限的，而数是无限多的。这个证明错在哪儿了呢？我也没办法一针见血地道出个所以然来，大家一起来讨论吧。

有趣的是，我们有一个与之相关的（正确的）定理：存在一个实数，它不能用有限个汉字来表达。这是因为，有限长的汉字字符串是可数的，而实数是不可数的。更有趣的是，这个定理的证明必然是非构造性的。

十三、两边同时取导数

两边同时取导数 (1)

取一个正整数 N 。则有
N² = N + N + N + … + N （ N 个 N ）
两边同时取导数，有
2N = 1 + 1 + 1 + … + 1 = N
两边同时除以 N ，得
2 = 1
数学威武！

这个推理是有问题的（废话）。随着 N 的增加，等式右边的 N 的个数却没变，因此 N² 的增长率比等式右边更大。

两边同时取导数 (2)

令 x = 1 ，两边同时取导数， 1 = 0 。哈哈！问题出在哪儿？这里有意略去答案不写，呵呵。

十四、链式法则也出错？

下面这个例子告诉我们，数学符号混淆不得，分清每个数学符号的意义有多重要。

定义 f(x, y) := (x + y)² ，然后令 x = u – v ，令 y = u + v 。我们有：
∂f/∂x = ∂f/∂y = 2(x + y)
∂x/∂v = -1
∂y/∂v = +1

根据链式法则，有
∂f/∂v = (∂f/∂x)·(∂x/∂v) + (∂f/∂y)·(∂y/∂v)
= 2(x + y)·(-1) + 2(x + y)·(1)
= 0

但是， f(u, v) = (u + v)² ，因此 ∂f/∂v = 2(u + v) = 2y 。这岂不是说明 y = 0 了么？但是，条件里并没有什么地方规定 y = 0 呀？这怎么回事？

问题出在，整个推理过程把两个不同的函数都用 f 来表示了。事实上，一个函数是 f(x, y) := (x + y)²，另一个函数是 F(u, v) = f(u – v, u + v) = (2u)² 。链式法则求的并不是 ∂f/∂v ，而是 ∂F/∂v 。

十五、不定积分的困惑

我们尝试用分部积分法求解 ∫ (1/x) dx 。
令 u = 1/x ， dv = dx
du = -1/x² dx ， v = x
于是 ∫ (1/x) dx = (1/x)x – ∫ x(-1/x²) dx = 1 + ∫ (1/x) dx

怎么回事？不怎么回事。这个等式是成立的。别忘了，不定积分的最后结果要加上一个常数 C 。

记得学高数时，求一积分，两哥们儿做出来的答案差别很大，而且试了很久也没能把其中一个答案变形成另外一个。后来终于恍然大悟：他们的答案是有可能不相同的，可以差一个常数嘛！

十六、貌似漏掉了什么

很多 Goldbach 猜想、孪生素数猜想的“证明”都栽在了下面这个有时候很不容易注意到漏洞。

让我们来证明一个看上去有些不可思议的结论： π^e 是一个有理数。首先注意到，对任意有理数 r ， logπr 都是无理数，否则令 s = logπr ，我们就有 π^s = r ，这与 π 是超越数矛盾。

现在，假设 π^e 是无理数，也就是说对任意有理数 r ， π^e 都不等于 r 。这也就是说，对任意一个 r ， logππ^e 都不等于 logπr 。由前面的结论， logππ^e 就不等于任意一个无理数。但 logππ^e 是等于 e 的，这与 e 的无理性矛盾了。因此，我们的假设是错的—— π^e 是一个有理数。

对于有理数 r ， logπr 确实是无理数；但遍历所有的有理数 r ，并不能让 logπr 遍历所有的无理数，而 e 正好就等于某个漏掉的无理数。

不过，也不要想当然地认为， π^e 当然是一个无理数。目前为止， π^e 是否有理还是一个谜。

声明：文章转自Matrix67博客，版权归原作者所有，转载仅供学习使用，不用于任何商业用途，如有侵权请联系删除，谢谢。