紧接着,我们想问:是否任意一个多边形内都能找到内接矩形呢?有意思的是,答案也是肯定的。但此时,前一节我们用到的两种证明方法现在都派不上用场了,我们需要用到一些全新的手段。下面这个证明真可谓是巧妙到了诡异的地步,真不知是谁想出来的。
对于多边形边界上的任意两点 A(x1, y1) 、 B(x2, y2) ,作出它们在三维空间中所对应的点 ((x1+x2)/2, (y1+y2)/2, √(x1-x2)2+(y1-y2)2) 。换句话说,把多边形放在水平面 z=0 上,对于多边形上的每一组无序点对 A 、 B ,在线段 AB 中点的正上方 |AB| 处作一个点。再把这个多边形本身加进去,我们就得到了一个三维空间中的封闭曲面。
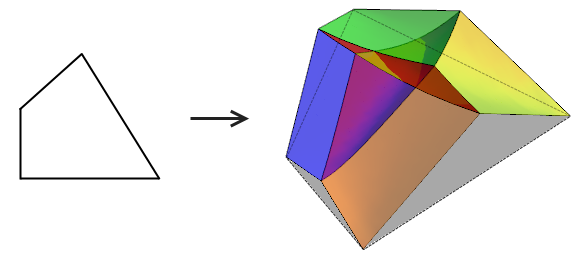
图1
可以看到,图中所示的例子中,这个曲面与自身相交了。这就表明,存在多边形边界上的两组点对 A 、 B 和 C 、 D ,它们满足线段 AB 和 CD 的中点重合,并且两线段一样长。这样,四边形 ABCD 就是多边形的一个内接矩形了。下面我们将说明,这个曲面一定会与自身相交。
容易看出,如果 A 、 B 两个点都在多边形的同一条边上,那么所有这样的点对在三维空间的对应点集是一个三角形;如果 A 、 B 来自于两条不同的边,那么所有可能的线段 AB 的中点将构成一个平行四边形,它们在空间中对应的点集就是一个有四条边的曲面。也就是说,这个曲面有一个 n 边形(底面),有 n 个三边形(对应多边形的 n 条边),还有 n(n-1)/2 个四边形(对应多边形的 n(n-1)/2 对边)。因此,这个曲面一共有 1 + n + n(n-1)/2 个面,而它的边数则为
(1/2) * (n*1 + 3*n + 4*n(n-1)/2) = n2 + n
另外,多边形的每两个顶点对应了曲面上的一个顶点,再加上底面上还有 n 个顶点,因此这个曲面有 n + n(n-1)/2 个顶点。于是,这个曲面的 Euler 示性数 V – E + F 等于
n + n(n-1)/2 – n2 – n + 1 + n + n(n-1)/2 = 1
这表面这个曲面是不可定向的,它不能嵌入到三维空间中。
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











