数学无处不在。说到植物中的数学,我们曾讲过斐波那契数列,讲过螺线,本文讲一讲荷花的果实——莲蓬中的数学。

图1
先看一个被称为“大圆套小圆”的数学问题:平面上有互不重叠的n个单位圆(n>1),应该如何摆放它们的位置,使得如果用一个最小的大圆包含它们,该大圆的面积最小?换句话说,在桌面上,应该如何摆放硬币,使得它们最密集?
如果n趋近于无穷,即为二维的最密堆积问题。已经证明其最密的情形如下图所示(这很符合直觉),密度不难计算,为
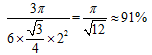
而三维情况即开普勒猜想:三维球堆的最大密度为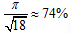 。
。
其提出400年来,直到去年才由匹兹堡大学的数学教授托马斯·黑尔斯彻底证明。
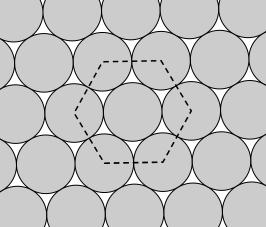
图2
回到我们最初的问题。容易理解,当n=2时,两个硬币应该相切;当n=3时,三个硬币应该两两相切……下图列出了n=2到9时的摆放方式:
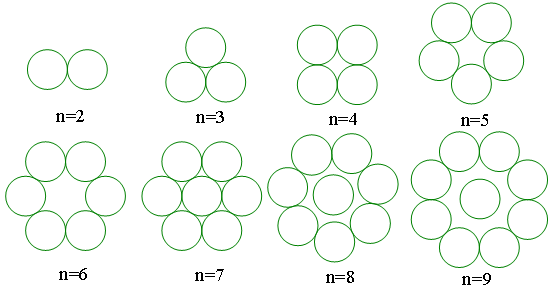
图3
其中n=6时,也可以将一个圆放到中间去;n=8和9时,中间的圆可以移动。而当n=13时,其摆放方式是外面9个圆,里面4个圆,如左下图:

图4
而这与13颗莲子的生长方式非常相似(如右上图)。数学家们还发现,不止13颗,其他颗数的莲子的生长方式基本也和数学上的解相对应。为什么莲蓬会这样生长呢?仔细一想不难明白,这样是最能节省原材料和空间的生长方式。真是妙哉!
然而,至今数学家们只解决了数十个n的情况,并且这个问题进展缓慢,基本上是平均2-3年解决一个n的值。
与此相关的另一个问题是,在某一足够大的给定区域(比如长方形)内,最多能放多少个单位圆?拓展到三维情况呢?问题就可能变得非常复杂,因为这时的排列方式未必是规律的,而可能是杂乱无章的。
参考文献:
[1] 花叶序背后的数学与物理.曹则贤.上海科普大讲坛第88讲
[2] 开普勒猜想.知乎网
[3] 百度百科
[4] 历史上的今天
声明:文章转自【52数学网】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











