Dan Christensen发现,把所有次数不超过5的、系数在-4到4范围内的整系数多项式的所有根描绘在同一个复平面上,你会看到一个异常壮观的画面。图中的每个灰色点代表某个二次多项式的一个根,蓝色点代表三次多项式的根,红色代表四次多项式的根,黑色代表五次多项式的根。水平线代表实轴,0和±1的地方有很明显的空洞;竖直方向是虚轴,每个单位根处也都有明显可辨的空洞。
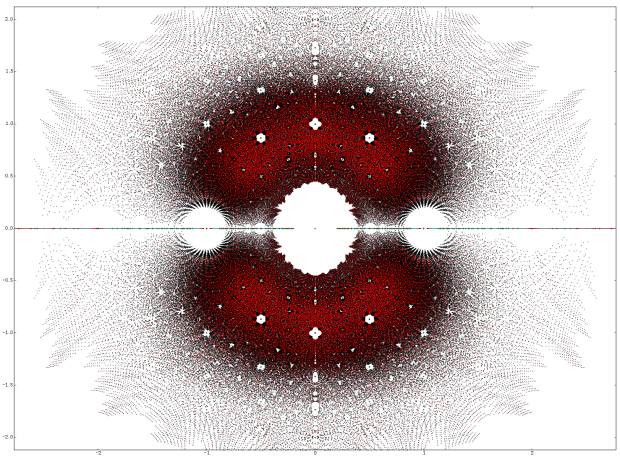
图1
受到上述实验的启发,Sam Derbyshire决定画一张更一般的、分辨率更高的多项式复根图。考虑每个系数要么为1要么为-1的全体24次多项式,它们总共将产生24*224——约等于4亿——个根。他让Mathematica运行了四天四夜才算出所有这些根的位置,得到了大约5个G的数据。最后,他用一个Java程序画出了这些根在复平面上的分布图,奇迹出现了:

图2
下面是一张局部放大图:

图3
这是位于1附近的局部放大图:
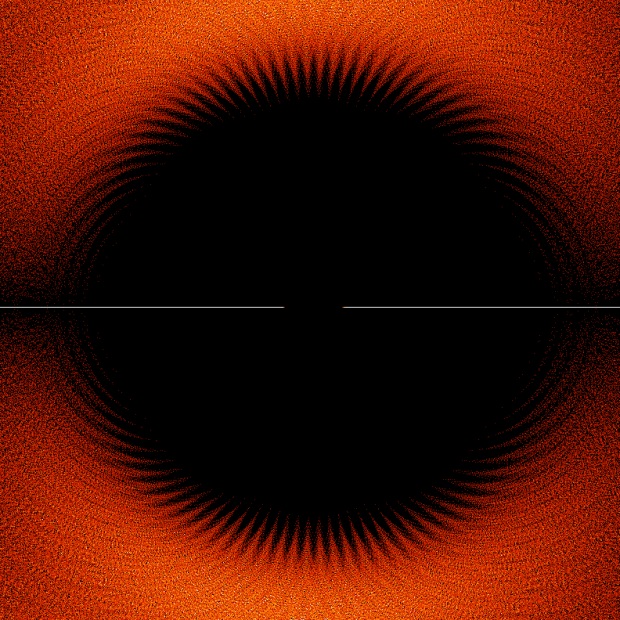
图4
这是位于4/5附近的局部放大图:
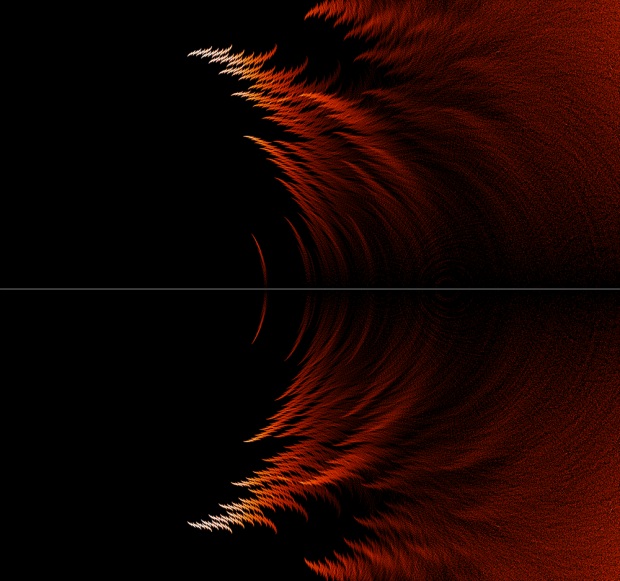
图5
这是位于(4/5)i 附近的局部放大图:
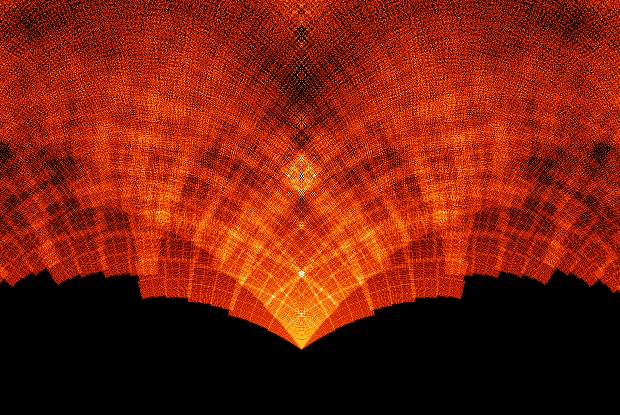
图6
最美的地方还是(1/2)*Exp(i/5)附近的局部放大图:

图7
查看更多:http://math.ucr.edu/home/baez/roots/
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











