连续函数f(x)满足f(0)=0且f(1)=0。证明,总能在[0,1]中找到两个数a和b满足b-a=1/2且f(a)=f(b)。换句话说,我们总能画出一条长为1/2的水平线段,它的两个端点都在函数f(x)上。
这个证明再次用到了我们上次提及的零点定理。考虑f(1/2)的值,如果它也等于0,我们的问题就直接解决了。无妨设f(1/2)>0,那么考虑f(x+1/2)-f(x)的值:当x=0时,该值为一个正数;但当x=1/2时,这个值变成了一个负数。这表明,在x从0增长到1/2的过程中,一定有某一刻使得f(x+1/2)-f(x)恰好为0。
我们接下来的问题是,除了长为1/2的横线段始终存在以外,还有哪些长度值具有相同的性质?下面我们证明,对任意一个正整数n,长为1/n的横线段也总是存在的。
我们先来看这么一个引理:如果在某个连续函数上不存在长为a的横线段,也不存在长为b的横线段,那么长度为a+b的横线段也是不可能存在的。为了证明这一点,只需要意识到:f(x)上存在一条长为a的横线段,当且仅当把f(x)向左(或向右)平移a个单位后,新的曲线与原来的曲线有交点。由于f(x)上不存在长为a的横线段,因此将f(x)右移a个单位后,新的曲线(图中的紫色曲线)与f(x)没有交点;类似地,将f(x)左移b个单位后,得到的绿色曲线与原曲线也没有交点。于是,绿色曲线和紫色曲线也不可能有交点,因为它俩被中间的那条蓝色曲线f(x)隔开了。而绿色曲线和紫色曲线相距a+b个单位。这就告诉我们,长为a+b的横线段也是不存在的。
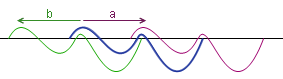
图1
现在,假如长为1/n的横线段不存在,我们立即推出长为2/n的横线段也不存在。我们进一步推出,长为3/n的横线段也不存在。依此类推,直至我们得出长为n/n = 1的横线段不存在,但这明显是错误的。
那么,对于长度值为其它数的情况呢?有趣的是,除了这些正整数的倒数以外,对于其余的任意一个长度值L,我们都能给出一个满足f(0)=0且f(1)=0但不含有长为L的横线段的连续函数。事实上,这个函数是。例如,函数就不含有长度为0.3的横线段。把该曲线向右平移0.3个单位,它与原曲线没有任何交点。
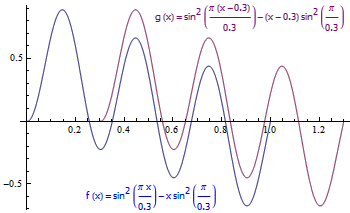
图2
我们可以由下面的推导看出,把这个函数水平平移0.3个单位实质上相当于是竖直平移了常数个单位,这就证明了平移前后的两条曲线的确没有交点。
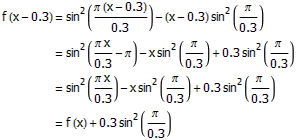
图3
那么,为什么当L等于某个正整数的倒数时,上面的函数就不管用了呢?关键就在于,如果L是一个正整数的倒数,上面的推导中最后的那个常数就不是非零常数了。
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











