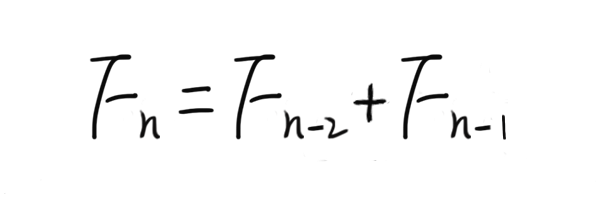
图1
本文节选自《人类最美的54个公式》
股神,其实都懂数学
视频1
零、股市操盘的“第一定律”
万物皆有灵性,吉卜赛人用嘶哑的嗓音宣告:需要唤起它们的灵性。这是《百年孤独》中开篇首页的一句对话。
如果说股市亦有灵性的话,那么,开启K线图灵性的钥匙就是斐波拉契数列。
斐波拉契数列一直被认为是大自然中的神奇异数。
它的相邻两项之商趋近黄金分割0.618,与之相关的0.191、0.382和0.500等数字,构成了股市中市场时间和空间计算的重要节点。
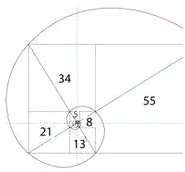
图2
金融市场的时间和价格服从斐波拉契数列,有时准确率达到十分惊人的程度。
当然,被操纵的内幕消息有时也会污染斐波拉契数列,但从大数据来看,股市k线图的走势与这个公式有着奇妙的联系。
我们假设股市是个理想模型(法律化、市场化),仅仅从数学层面,谈一谈这个被股市操盘手应用,同时也被巴菲特、索罗斯推崇、敬畏的神秘数列。它为什么成为股市操盘手遵循的“第一定律”?
一、诡秘美丽的斐波拉契数列
一般认为斐波那契数列的提出是基于兔子的繁殖问题:如果一开始有一对兔子,它们每月生育一对兔子,小兔在出生后一个月又开始生育且繁殖情况与最初的那对兔子一样,那么一年后有多少对兔子?
答案是,每月兔子的总数可以用以下数列表示:1,1,2,3,5,8,13,21,34,55,89,144,233…
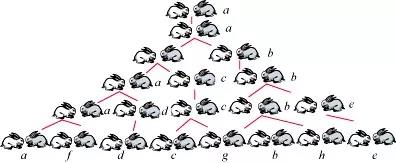
图3
这一数列是意大利数论家列奥纳多·斐波拉契(Leonardo Fibonacci)在他13世纪初的著作Liber Abaci中最早提出的。如果取数列前两个元素为1,那么递推关系就是:
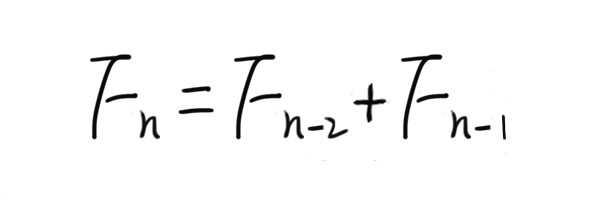
图4
这列数字乍看起来似乎没有规律可循。
但仔细观察就会发现下一个数为前两个数之和。
所以可以用递归的方法定义公式:
F(0)=0,F(1)=1, F(n)=F(n-1)+F(n-2)(n>=2,n∈N*)
在数学信徒的眼中,数字总能产生无穷的美感,而斐波拉契数列是其中最美丽、最和谐的数字集合,他的后一个数字和前一个数字的比值,无限接近于黄金分割0.618,这就很有意思了,大到宇宙空间到小到原子夸克,从时间到空间,从自然到社会,总结它们的规律时都能找到斐波那契数的踪迹。
二、股市周期论:为什么选择斐波拉契数列作为参照系
关于数学的书基本都会提到斐波拉契数列,它几乎无处不在。
从自然万物来看,斐波拉契数列符合自然规律,是发展的最美结果的一组数列。
有人说,上帝用斐波拉契数列创造了整个世界(可以观看前面推荐的视频,美到极致)。
斐波拉契数列是大自然的美,也是数学本身的美。
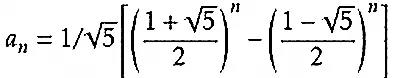
图5
选用斐波那契数列作为股市周期线是一种偶然也是一种必然。在用这个数列来进行推算时,得到市场大数据的认可,然后逐渐成为股市的金科玉律。
我们并不知道斐波那契数为什么与股市周期如此吻合,只能说冥冥之中,自有感应。
股市里的操盘手,公开发表的不管是文章还是内部报告,都只谈宏观、产业、公司基本面、财务等,尽可能把技术分析做在暗地。
在应用“斐波拉契数列”时,他们一般会遵循以下规则:
1. 只当有股市出现重大变故时,例如1999年“5.19”行情,2015年“6.28”行情,斐波拉契数列才完全从头开始加上0,否则从1开始,然后观察第2天,第3天,第5天,第8天的变化情况。这些数字作为关键节点位置,对未来的走势起决定作用。
2. 斐波拉契数列间隔周期越来越长,所以它反映的事件的影响也越来越弱,预测的敏感性也越来越低。因此一般只看到第34天或者55天,以后的影响会变得很小。
3. 一般可以选择把第13天作为新一轮的第一天,一般来说就算以后会出现大事件也会和周期内的一天重合。
4. 若根据几个不同的起始点事件推演下来,得到了连续好几天但不能确定时,一般会选择较前的那一天。
5. 斐波那契数列是横向周期,而黄金分割线是纵向周期,两者可以结合起来看。突破压力位的当天作为重新起始,记为1,继续观察后续的平整或突破。
6. 可以与其它数列结合使用,但优先考虑斐波拉契数列。
…………
三、神奇的吻合,斐波拉契数列在股市中的应用
“炒股者都懂数学”,这是华尔街操盘手的一句名言。
在许多人眼里,周期是一种玄乎的东西,特别是股市中的一些“神棍”例如李大霄的拙劣表演,还有一些人独创各种理论,既无数据支撑,更无理论基准。目标就是割韭菜,卖空气,骗傻子。
而斐波拉契数列,它是微观数据的一种宏观显示,就像大自然中的时间节奏、能量运动的基本节律一样,斐波拉契数列就是股市数据中跳动的和弦。
单个数据是无法预测的“布朗运动”,但作为一个整体,400年的股市历史和数据作为一个整体,其行为却必定呈现某些规律,从而可以预测。
以最近一支上市公司(不具体点名)的股票作为研究对象,说一下斐波拉契数列在股市中的应用,你会看到它的波动与斐波拉契数列有着神奇的吻合。其中的垂直线分别标志着未来第3、第8、第13、第21、第34、第55及第89个交易日的位置。这些日子可能意味着市场的重要转折点。
1. 利用斐波拉契数列时间窗口推算股票变盘点
如图从K线上看,从上市开始的第8、13、21、34个交易日均为市场重要的变盘点,尤其是画圈的最高点均恰好落在斐波拉契时间窗上。
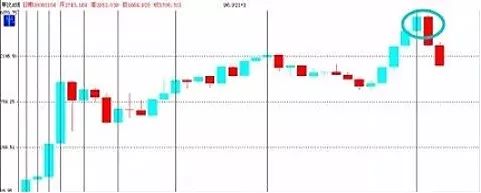
图6
从月线看,斐波拉契时间窗有效地预测出重要变盘点。
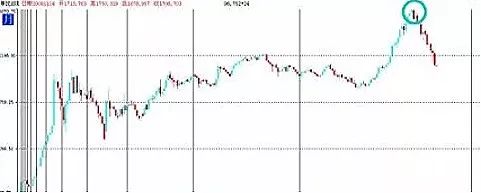
图7
从日线看,斐波拉契时间窗有效预测出重要变盘点。将鼠标放在最后一根竖线上,可显示下一个费氏时间窗在2389个交易日出现,离我们太远。
图8
我们可以以历史上已经被证实过的重要高低点为斐波拉契时间窗的起点。如图这一天点斐波拉契时间窗,可捕捉到变盘点。
图9
以在历史上被证明过的焦点为起点,所计算出的斐波拉契的变盘点成功率会更高。
利用斐波拉契回调理论观察股市,已经成为股市技术分析学的显学。
2. 斐波拉契弧的深度应用
除了基本的斐波拉契数列时间窗口,这数学史上最著名的数列与股票价格之间的联系,还有更多的研究,包括斐波拉契弧、斐波拉契扇形、斐波拉契回调和扩展。
我们这里以斐波拉契弧为例,再一步来验证这个数列并非浪得虚名。
斐波拉契弧是以趋势线的长度及其某一倍数为半径衍生的一系列半圆。第一、第三个弧分别基于0.382和0.618这两个斐波拉契比例,中间的那条弧线通常设定为趋势线的50%。
构造斐波拉契弧的第一步是在价格的两个极端值之间画出一条趋势线,比如一段时间内所达到过的最高价和最低价。随后,以第二个极端值所对应的点为圆心,画出三条弧线,其半径分别为趋势线长度的38.2%,50.0%和61.8%。
如下图所示,苹果的股价在经历了从2012年5月18日的522美元上涨至9月21的704美元的大牛市后,开始发生修正。在那一时刻,就可以利用这两个最高、最低价格画出斐波拉契弧。
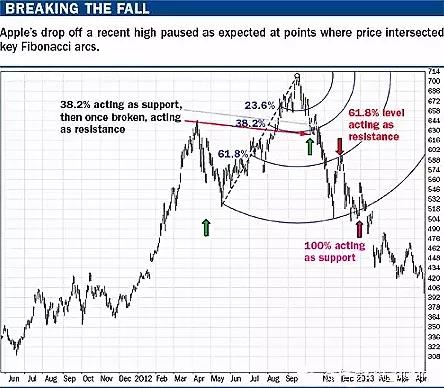
图10
总之,斐波拉契数列影响着股市运行的时间周期。
具体使用中,每到时间周期、神奇数列附近,需格外注意股市的涨与跌,大波段的时间周期如果同中小波段的时间周期重合或接近,更需要注意变盘与否。
斐波拉契数列在金融市场中几乎无处不在,加上变种“鲁卡斯数列”与之相互验证,使一些分析可以去“孤”从“众”,虽然不能说战无不胜,但肯定会比瞎买要靠谱得多,当然,你也可以不同意,那是因为你天生富贵命。
在股市这片黑幕沉沉的领域里,斐波拉契数列为散户指出一线光明。
四、人性战胜不了“斐波拉契数列”
那么问题来了,如果你懂了斐波拉契数列,是不是就成为了巴菲特2.0。
事实肯定并非如此,因为就算你弄懂了斐波拉契数列,你仍然没有办法按照它的节奏来操盘。
看过海浪吗?它有两种基本模式:一种是基本恒定的,每一个浪到来的时间大致等长。一种是由舒缓到急促,再从急促归于舒缓,从舒缓到急促或从急促到舒缓的时间间隔也是有一定规律的,比如每一个浪到来的时间都比前一个浪到来的时间提前或滞后0.5秒钟等等。两者构成了时间周期的基本模式。
这也是人的心理的基本模式,要么均匀分布,要么长尾效应。举个例子,如果你迷恋上了微博,一开始你可能平均10秒刷一下微博,那天当你失去兴趣,你可能登录的时间会越来越长,就是你在操盘的时候,有些人是天天要去买卖N次,否则心里就特别难受。有些人一开始操作非常密集,到后面撒手不管直至听天由命。
图11
可惜人性这两种心理模式都与斐波拉契数列并不吻合,如果没有强大的控制力,自己操盘总是与斐波拉契数列背道而驰,很多时候数学规则与人性总是相悖离的,所以性情的小燕子永远成不了巴菲特。
机构投资者表现要优秀得多,因为他们除了用到斐波拉契数列、艾略特波浪理论、凯利公式这些数学工具之外,他们一直在摆脱人性,让人性尽量远离股市的操作。
人性的心理波动没有办法与上帝的斐波拉契数列同步。
五、总结:再牛逼的技术,在中国股市也会亏到哭
以上所说内容,是建立在理想化股市模型之上,斐波拉契数列才能发挥最大效应。
如果股市本身是一个赌场,而且是一个被操纵的赌场,那它的很多数据已经被污染,斐波拉契数列就不会那么准确,这在中国的股市体现得特别明显,什么理论到了中国都是失效的。量子学派在另一篇《别去赌场了,你永远赢不了凯利公式》已经有非常详细的说明。
吴敬链曾将中国股市直接比喻为赌场,甚至认为前者还不如后者有规矩,赌场里有规矩的,比如你不能看别人的牌。而股市不一样,有些人是可以看别人的牌的,甚至可以作弊,普通股民可以说处在信息极端不对等的地位上。
就算你将斐波拉契数列发挥到极致,仍然也会亏到哭。
声明:文章转自【量子学派】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











