由单位正方形拼接而成的图形叫做多联骨牌(Polyomino)。一个有趣的问题是,能否用奇数个相同的多联骨牌拼成一个对称图形?答案是肯定的。下图显示了如何用奇数个相同的多联骨牌拼接出中心对称图形和沿对角线方向轴对称的图形。
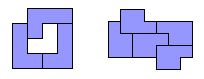
图1
下面的问题该轮到你来回答了。你能否用奇数个相同的多联骨牌拼接出一个左右轴对称的图形?当然,你所使用的多联骨牌本身必须是不对称的。为了方便起见,下文我们所说的“轴对称”均不再考虑沿对角线方向对称的情况。
五联骨牌共有12种。令人吃惊的是,对于上述问题,所有这12种骨牌都有至少一个解。其中长条形、十字架形、T字形和U字形这4种是本来就对称的。你能否找出其余8种五联骨牌的解?
并非所有的多联骨牌都是有解的,有一些六联骨牌就没有解。你能否找出一个没有解的多联骨牌,并证明它确实不可能有解?
其实,用奇数个相同的多联骨牌拼出左右轴对称的图形是完全有可能的,并且这样的情况非常之多。下面随便举几个例子。你刚才都想到了哪些?

图2
对于这个问题,8种非对称的五联骨牌都是有解的。下面就是这8个图形的解:
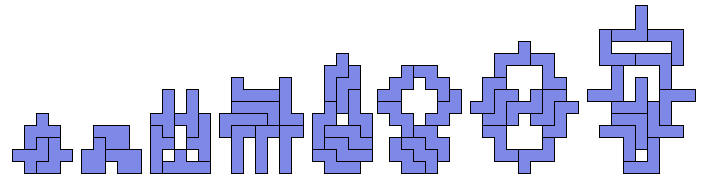
图3
下面我们证明,你永远不可能用奇数个h形六联骨牌排成一个左右轴对称的图形。
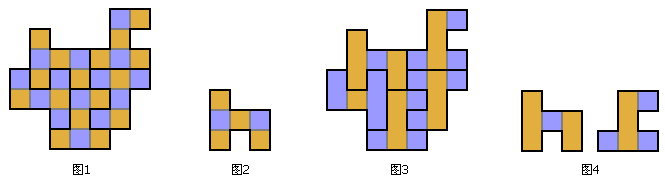
图4
像国际象棋棋盘一样对拼出来的图形进行染色(图1),你会发现同一块h形骨牌里两种颜色的格子数量始终不等(图2),奇数个骨牌加起来两种颜色的总格子数目显然也就不会相等;但一个沿格子边线轴对称的图形,两种颜色的格子应该一样多才对。现在的问题是,如果对称轴在格子内的中心线上咋办。为此,我们还需要对拼出来的图形进行带状染色(图3)。注意到不管这些骨牌怎么放,同一个骨牌中每种颜色的格子都是奇数个(图4),奇数个骨牌加起来,每种颜色的格子总数也都还是奇数个。而在拼接出来的图形里,对称轴所在的那些格子全是一种颜色,另一种颜色的格子则左右对称分布,这种颜色的格子数应该有偶数个才对。这样我们就证明了,用奇数个h形六联骨牌不能拼出轴对称的图形。
更多的结论可以在这里看到:http://www.monmouth.com/%7Ecolonel/oddities/index.html
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











