H.W.Richmond在1921年的第10期The Mathematical Gazette里提出了这样一个问题:任意写下一个数,再在它下面写下它的2倍、3倍、4倍、……、9倍。把这些数按位对齐,每一列里恰好有9个数字(前面几行中的首位为空时该位置视作0)。证明,每一列中至少有一个数字0或者数字9。
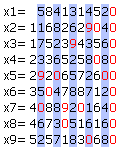
图1
设我们最初写下的数为S,则这9个数分别为S, 2S, 3S, …, 9S。假如某一列里任一个数字都不等于0或者9,这也就是说该列的所有9个数字都只能取1到8里的数,于是由鸽笼原理,必定存在两个数aS和bS,该位上的数字是相同的。不妨设a>b,于是,在aS-bS中,该位置上的数字必然只能是0或者9(这取决于它前面是否有借位),而aS-bS=(a-b)S显然也在这9行数里面。
题目来源:http://www.cut-the-knot.org/Curriculum/Arithmetic/ZerosAndNines.shtml
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











