今年恰逢PKU数学文化节十周年,其间开办的很多讲座我都去了。去听讲座的人好像都是数院的,我恐怕是唯一一个中文系的。考虑到我和中文系的MM没有共同话题,因此每一次听讲座时我都会顺便四处打望,看看有没有数院的美女,下来可以和她“交谈”一下。有趣的是我的做法与常人所想的恰好相反:据说数院的已经盯上中文系的MM了,而我一个中文系的竟然反过来去找数院的MM。
昨天有一个关于非欧几何的讲座,这是目前所有的讲座中最为精彩的一次。讲座里提到了Poincaré的一个双曲几何模型,感觉非常有意思,在这里和大家分享一下。
在所有的双曲几何模型中,Poincaré的圆盘模型可能是最有趣的一个。这个双曲世界存在于一个有限的平面区域里,整个世界限制在一个单位圆的范围内。这个世界中有两个最重要的物理定律:一,假如某物体X离原点O距离为d,那么该物体的温度为1-d2;二,物体的大小与温度成正比。这样,假如某个人从这个世界的中心走向边缘,那么他的温度会从1慢慢变成0,同时整个人慢慢变小。他自身大小改变的同时周围的物体也等比例地放大或缩小,而这个世界里的人视野有限,看不见远处的东西,因此他不会觉得自己变小了或者变大了。因此,在这个世界里,物理学家们能够很轻易地发现第一定律,但要发现第二定律则非常具有挑战性,探索第二定律的过程必然很曲折,并且很可能出现哥白尼时代的故事。
对于我们来说,这个世界是有界的;但对于这个世界中的人来说,这个世界是无穷大的。因为离原点越远,人就越小,于是相对来说他们所看到的空间也就越大。当人的位置趋于边界时,物体大小趋于0,此时的空间将变得无穷大,因此这个世界中的物体永远无法到达边界。同时,离原点越远的话越接近“绝对零度”,这将非常不适宜生物的生存,因此人们大多居住在原点,离原点越远城市规模越小,更远的地方则完全没有开发过,只适合于疯狂的冒险家进行极限运动。于是这个世界中的物理学家很自然地得到这个结论:世界是无穷大的。
下面就神奇了。现在,考虑某个人想从A点走到B点。如果按照红色的线段直直地走过去,所走的路程并不是最短的,因为这条路线离原点较远。聪明的人会发现,我先往原点方向走一点,然后再到B点去,这样走的路程更短一些。我们猜想,最短路线很可能是一条偏向于原点的弧线(就好像原点把直线段“吸”过去了一样)。之所以产生这种奇怪的现象是因为,离原点越远物体就越小,人的步子也变小了,相对来说实际空间就变大了。因此,对我们来说距离相等的两点,对他们来说离原点越远其实际距离越大。因此,我们有必要重新定义这个双曲世界中“距离”的概念。由于物体大小与1-d2成正比,因此我们可以定义,如果在离原点距离为d的位置上有一个充分小的位移,在我们看来距离为Δx,那么在这个世界中的实际距离就是Δx/(1-d2)。这样就可以算出,从A到B的最近路线是一条垂直于边界的圆弧(蓝色的那条)。于是在这个世界中,“直线段”已经不再是我们熟悉的直线段了,而是一条条的弧线(还包括整个圆的直径)。而我们眼中的直线,在他们看来就是曲线。
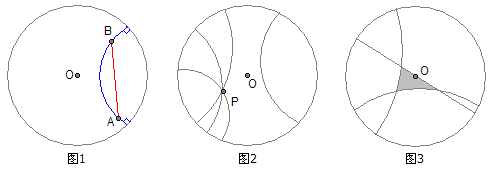
图1
这个世界中的几何满足欧式几何的前面四个公设,但不满足第五公设。比如,两点确定一条直线,因为过两点的圆弧只有一条垂直于这个世界的边界;而直线可以无限延长,因为离边界越近两点的实际距离越大,你永远走不到尽头。但是,这个世界不满足第五公设。从图2可以看到,过一点可以作无数条直线不与已知直线相交;从图3可以看到,三角形的内角和小于180度。下面这幅图片可以帮助你更好地理解这个双曲模型。这是该平面上的一个三角形剖分,里面的所有三角形都是等边三角形,而且所有这些三角形都是一样大的。你可以看到7个等边三角形共用一个顶点,这说明三角形的内角和小于180度。

图2
另外值得一提的是,这个构想很适合写成一篇科幻小说。记得大刘的那篇科幻吗?一群电子器件诞生在某颗星球的内核,然后探索物理定律,历经重重困难,最终冲破了它们那个世界的“天然外壳”,看到了外面的世界,并相信我们整个宇宙也处于一个更大的星体内。这个双曲几何模型也很适合写出这样的小说来,比如以物理史书的方式叙述从古至今若干个传奇人物的故事,讲述他们是如何从一些奇怪的现象出发,通过各种试验证明自己的猜想,顶住社会各方面的压力,执著地探索宇宙的奥秘。小说中的人物可以带着读者一起进行探索,最后才告诉读者这个宇宙的本质是什么。
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











