
很多东西都是吹神了的,其中麦田圈之谜相当引人注目。上个世纪里人们时不时能听见某个农民早晨醒了到麦田地一看立马吓得屁滚尿流的故事。上面这幅图就是97年在英国Silbury山上发现的麦田圈,看上去大致上是一个雪花形状。你或许会觉得这个图形很好看。看了下面的文字后,你会发现这个图形远远不是“好看”可以概括的,它的背后还有很多东西。
在说明什么是分形艺术前,我们先按照下面的方法构造一个图形。看下图,首先画一个线段,然后把它平分成三段,去掉中间那一段并用两条等长的线段代替。这样,原来的一条线段就变成了四条小的线段。用相同的方法把每一条小的线段的中间三分之一替换为等边三角形的两边,得到了16条更小的线段。然后继续对16条线段进行相同的操作,并无限地迭代下去。下图是这个图形前五次迭代的过程,可以看到这样的分辨率下已经不能显示出第五次迭代后图形的所有细节了。这样的图形可以用Logo语言很轻松地画出来。
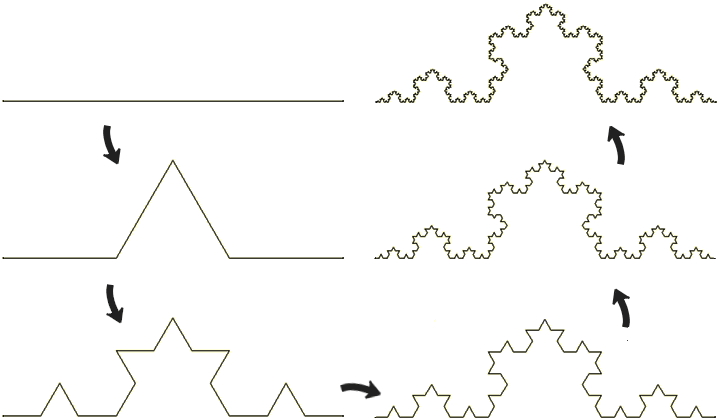
图1
你可能注意到一个有趣的事实:整个线条的长度每一次都变成了原来的4/3。如果最初的线段长为一个单位,那么第一次操作后总长度变成了4/3,第二次操作后总长增加到16/9,第n次操作后长度为(4/3)n。毫无疑问,操作无限进行下去,这条曲线将达到无限长。难以置信的是这条无限长的曲线却“始终只有那么大”。
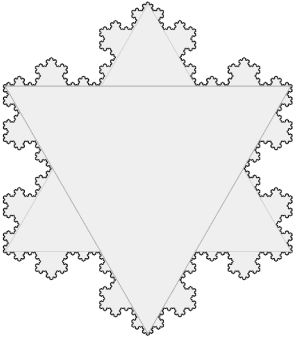
图2
当把三条这样的曲线头尾相接组成一个封闭图形时,有趣的事情发生了。这个雪花一样的图形有着无限长的边界,但是它的总面积却是有限的。换句话说,无限长的曲线围住了一块有限的面积。有人可能会问为什么面积是有限的。虽然从上面的图上看结论很显然,但这里我们还是要给出一个简单的证明。三条曲线中每一条的第n次迭代前有4n-1个长为(1/3)n-1的线段,迭代后多出的面积为4n-1个边长为(1/3)n的等边三角形。把4n-1扩大到4n,再把所有边长为(1/3)n的等边三角形扩大为同样边长的正方形,总面积仍是有限的,因为无穷级数Σ4n/9n显然收敛。这个神奇的雪花图形叫做Koch雪花,其中那条无限长的曲线就叫做Koch曲线。他是由瑞典数学家Helge von Koch最先提出来的。本文最开头提到的麦田圈图形显然是想描绘Koch雪花。
分形这一课题提出的时间比较晚。Koch曲线于1904年提出,是最早提出的分形图形之一。我们仔细观察一下这条特别的曲线。它有一个很强的特点:你可以把它分成若干部分,每一个部分都和原来一样(只是大小不同)。这样的图形叫做“自相似”图形(self-similar),它是分形图形(fractal)最主要的特征。自相似往往都和递归、无穷之类的东西联系在一起。比如,自相似图形往往是用递归法构造出来的,可以无限地分解下去。一条Koch曲线中包含有无数大小不同的Koch曲线。你可以对这条曲线的尖端部分不断放大,但你所看到的始终和最开始一样。它的复杂性不随尺度减小而消失。另外值得一提的是,这条曲线是一条连续的,但处处不光滑(不可微)的曲线。曲线上的任何一个点都是尖点。
分形图形有一种特殊的计算维度的方法。我们可以看到,在有限空间内就可以达到无限长的分形曲线似乎已经超越了一维的境界,但说它是二维图形又还不够。Hausdorff维度就是专门用来对付这种分形图形的。简单地说,Hausdorff维度描述分形图形中整个图形的大小与一维大小的关系。比如,正方形是一个分形图形,因为它可以分成四个一模一样的小正方形,每一个小正方形的边长都是原来的1/2。当然,你也可以把正方形分成9个边长为1/3的小正方形。事实上,一个正方形可以分割为a2个边长为1/a的小正方形。那个指数2就是正方形的维度。矩形、三角形都是一样,给你a2个同样的形状才能拼成一个边长为a倍的相似形,因此它们都是二维的。我们把这里的“边长”理解为一维上的长度,那个1/a则是两个相似形的相似比。如果一个自相似形包含自身N份,每一份的一维大小都是原来的1/s,则这个相似形的Hausdorff维度为log(N)/log(s)。一个立方体可以分成8份,每一份的一维长度都是原来的一半,因此立方体的维度为log(8)/log(2)=3。同样地,一个Koch曲线包含四个小Koch曲线,大小两个Koch曲线的相似比为1/3,因此Koch曲线的Hausdorff维度为log(4)/log(3)。它约等于1.26,是一个介于1和2之间的实数。
我们常说分形图形是一门艺术。把不同大小的Koch雪花拼接起来可以得到很多美丽的图形。如果有MM看了前面的文字一句也不懂,下面这些图片或许会让你眼前一亮。
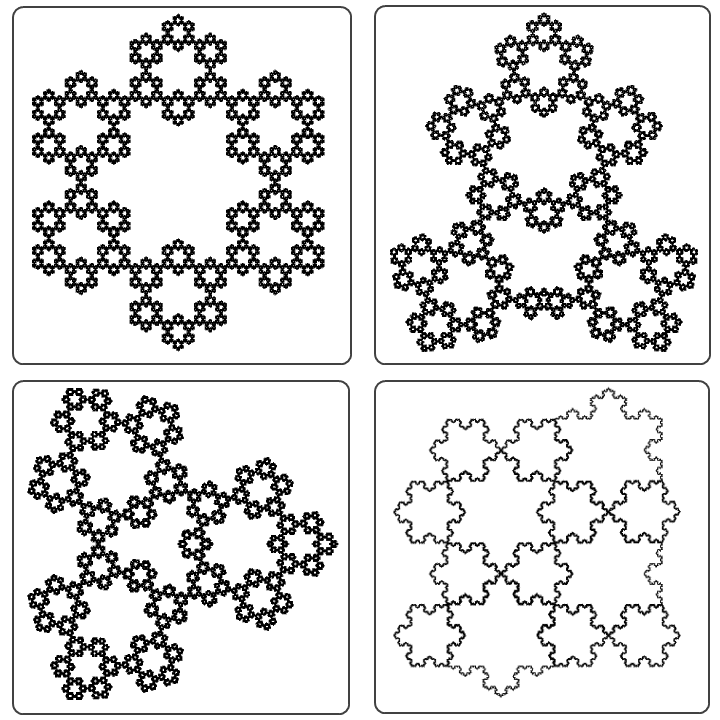
图3

图4
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











