康托集合是闭区间[0,1]的子集,它的定义如下:给定区间[0,1],把这个区间分成三段,去掉中间那一端(即去掉(1/3,2/3)),然后把剩下的两段中每一段都按照刚才的方法再进行操作,然后再分,再分,就这样一直挖洞挖下去。在第二次操作后,剩下的区间是[0,1/9]∪[2/9,1/3]∪[2/3,7/9]∪[8/9,1],再操作一次后区间将由8段构成。最后剩下来的东西是什么呢?你能找到存在于这个集合中的某个具体的元素吗(不包括形如x/(3n)的端点)?
我们看到,n次操作后,区间的总长度为(2/3)n,当n趋于无穷时,区间长度趋于0。但是这并不能说明这个区间里没有任何元素。事实上,我们可以找到至少一个元素。比如,下图中绿色的点表示三等分点,如果P满足AP/AB=A'P/A'B'的话,那么P点始终以比例相同的位置留在某一段上,这样的话即使无限地分下去也不会把它挖掉。
图1
P点的坐标可以通过解这个方程得到:x/1=(x-2/9)/(1/9)。解出来x为1/4。因此,1/4属于康托集合。当然,除了1/4之外还有很多点在这个集合内,我们只是找到了其中一个。事实上,康托集合内的元素有无穷多个。假如我们把所有0到1的数用三进制表示,那么我们发现,去掉的部分都是三进制小数里有数字“1”的。比如,第一次操作时,1/3和2/3的三进制分别是0.1和0.2,我们去掉的是所有从0.1到0.2的数(不包含端点,因为0.1也可以写成0.0222222222…)。第二次操作就去掉了百分位有1的那些数,依此类推。因此,只要一个位于0和1之间的三进制小数能够只用0和2写出,那么它就属于康托集合,因为它永远不会被去掉。刚才的1/4转化为三进制是0.020202…,因此它属于这个集合。显然,这样的数有无穷多个,比如三进制0.002002002…等于十进制的1/13,因此它也属于康托集合。同样,康托集合里不存在孤点,因为在它的左右可以找出无数个属于康托集合的数。应用对角线方法,这个集合里的元素居然还是不可数的。事实上,我们可以建立康托集合与闭区间[0,1]的一一对应关系。
用以下方法可以把康托集合里的所有数与[0,1]的所有实数对应起来:将康托集合内的任意一个转化为三进制小数后,把每一个数字除以2,再当成是二进制小数转化回来。由于这些三进制小数里只含0和2,因此康托集合里的每个数都恰好能转化为一个[0,1]之间的二进制小数;同样地,二进制小数里的每个“1”变成“2”后也能得到一个康托集合里的数。
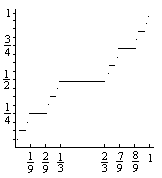
图2
设f为定义域在康托集合内的函数,定义f(x)为按照上面的转化方法x所对应的二进制小数,显然这个函数的值域就是[0,1]。比如1/3的三进制为0.0222…,而二进制0.01111…=0.1即十进制的1/2,因此f(1/3)=1/2。我们发现,2/3的三进制为0.2,而0.1的十进制也是1/2。于是f(1/3)=f(2/3)。类似地,那些被挖去的区间的两个端点对应的函数值都相同。现在,我们把这个函数的定义域也扩展到[0,1]:让康托集合里的那些被挖去的区间里的点的函数值与该区间对应的端点相同(在函数图象上看相当于把函数值相等的点用横线段连起来)。于是,f(1/2)=f(1/3)=f(2/3)=1/2,f(1/8)=f(1/9)=f(2/9)=1/4。这个函数一定是上升函数,它在长度为1的区间里从0增长到了1。同时,这个函数也是一个连续函数,因为康托集合与[0,1]的所有实数一一对应。这个函数是一个阶梯状的函数,但是它不是分段的,是连续的。它是无穷多个横线段组成的一个连续函数,除端点无意义以外导数值都是0。或者说,这个函数在不变之中上升。
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。