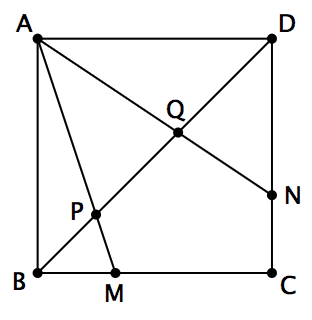
图1
四边形 ABCD 是一个正方形,在 BC 上取一个点 M ,在 CD 上取一个点 N ,使得 BM = CN 。连接 AM 、 AN ,与对角线 BD 分别交于 P 、 Q 两点。求证: BP 、 PQ 、 QD 三条线段一定能组成一个三角形,并且这个三角形的其中一个角等于 60° 。
其中一种思路就是,借助一些辅助线,在图中弄出一个含 60 度的三角形来,并说明它的三边长度就是 BP 、 PQ 、 QD 。但问题的难点就是,我们上哪儿找一个含 60 度的三角形?在很多平面几何问题中,把图形扩展到三维空间中去,反而会带来意想不到的突破(可以参见这里和这里)。现在,我们又有了一个绝好的例子。
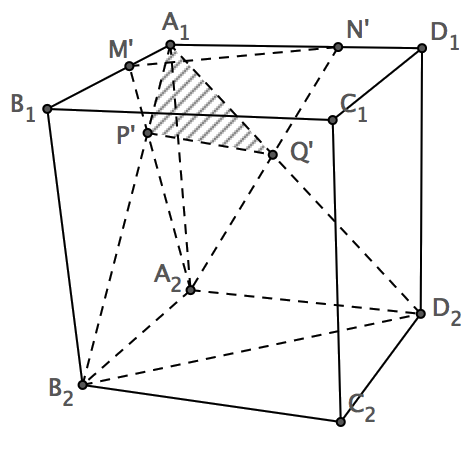
图2
如图,作一个边长与正方形相等的正方体 A1B1C1D1 – A2B2C2D2 ,在 A1B1 上截取 A1M’ = BM ,在A1D1 上截取 A1N’ = DN 。假设 A1B2 和 A2M’ 交于点 P’, A1D2 和 A2N’交于 Q’ 。注意到三角形 A1B2D2 的三条边都相等,因而它是一个等边三角形, ∠B2A1D2 = 60° 。如果图中阴影三角形的三边长度分别等于 BP 、 PQ 和 QD ,问题就解决了。显然, A1P’ = BP , A1Q’ = QD ,因此我们只需要说明 P’Q’ = PQ 。
容易证明, M’N’ = MN , A2M’ = AM , A2N’ = AN ,因此三角形 A2M’N’ 和三角形 AMN 全等,于是 ∠M’A2N’ = ∠MAN 。另外,容易看出 A2P’ = AP , A2Q’ = AQ ,而刚才我们已经证明了 ∠M’A2N’ = ∠MAN ,于是三角形 A2P’Q’ 与三角形 APQ 全等。于是, P’Q’ = PQ 。
题目出自单遵《平面几何中的小花》。
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











