图1
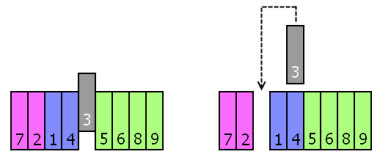
书架的某一层里放了一套百科全书,但它们排列的顺序却是乱的。一个傻子想要把这套书排好顺序,也就是说他想要书架里的书从左至右分别是第 1 卷,第 2 卷,……,第 n 卷。他给这套书排序的办法是这样的:不断取出一本原应放在更左边的书,插进它该在的位置。比方说,某本书的卷号是 3 ,它的位置却是左起第 5 ,位于其目标位置的右侧。那么傻子就可以把这本书拿出来,插入当前左起第 2 本书的右边,把那些占了它位置的书挤到更右边去,而不管这一操作是否会破坏掉已经就位的书。注意到这种排序法很可能捡了芝麻,丢了西瓜,为了一本书的位置而破坏掉一连串原已排好的书,可谓是鼠目寸光,缺乏远见。我们的问题是,在哪些情况下这样的排序法最终一定能实现排序,哪些情况下可能会陷入永无止境的死循环?
出人意料的是,这种看上去明显有漏洞的排序法竟然是一种正确的排序算法——对于任意一个初始序列,采用这种方法总能让序列最终变得有序。为了证明这一点,我们按照如下方式把序列编码为 n 位的 01 串:左起第 i 位为 1 当且仅当第 i 卷在正确的位置上。序列 7, 2, 1, 4, 3, 5, 6, 8, 9 就被编码为 010100011 ,因为在这 9 本书当中,只有卷 2 、卷 4 、卷 8 和卷 9 在正确的位置上。
如果某一次操作中,傻子把第 k 卷放进了正确的位置,那么考虑所有卷数小于 k 的书:如果它原本就在左起第 k 本书的左边,这个操作影响不到它;如果它原本就是左起第 k 本或者更右边的书(这表明它原本就不在正确的位置上),那么现在它仍然不可能在正确的位置上(它的位置只可能不变或者更靠右了)。因此,编码的前 k-1 位是不动的,但第 k 位从 0 变成 1 了。这就意味着,任意一个操作总会让整个二进制编码变大。而容易看出,只要序列不是有序的,傻子总有可以操作的对象,因此序列编码将不断增加,最终将变成 111…11 。此时所有书都在它应该在的位置上,整个序列也就有序了。
现在,又来了另外一个傻子。他的排序办法和前一个傻子基本上相同,唯一不同的是,他每次都可以选择任意一本不在原位的书(并把它放进它应该在的位置),而不仅仅是选择那些位于目标位置右侧的书。这个傻子的排序方法还能保证最终总会让这排书变得有序吗?
答案竟然再一次是肯定的——这种方法最终总能让所有序列变得有序。为了证明这一点,只需要注意到,只要序列不是有序的,傻子总能找到合法的操作,因此只要不存在循环,序列最终一定会变得有序。我们将用反证法证明,傻子的操作一定不会让状态产生循环。
假设存在一个循环,并且在某一步,傻子取出了第 k 卷,并且无妨假设它被移动到了更右边的某个位置。由于这是一个循环,因此在某个时候它又跑回了目标位置的左边。这说明,傻子一定取出了一本卷号比 k 更大的书,放到了 k 的右边,并把 k 挤到左边去了。只需要令 k 为循环中被挪到右边的书中卷号最大的一本,矛盾就产生了。
我们自然会提出这样一个问题:这种排序算法的效率如何?换句话说,最坏情况下傻子排序法需要操作多少步?今年一月和二月的 UyHiP 谜题中, Michael Brand 详细地讨论了这个问题,有兴趣的朋友可以看看:
[1] http://www.brand.site.co.il/riddles/201001q.html
[2] http://www.brand.site.co.il/riddles/201002q.html
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











