这是一个经典智力问题,不知道大家见过没。下图是一辆自行车在泥地中驶过留下的痕迹,你能据此判断出这辆自行车是从左往右行驶的还是从右往左行驶的吗?
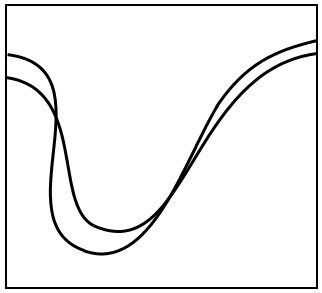

图1
提示:题目条件是充分的,根据这两道车轮印我们足以判定车行方向。这和图中的线条粗细、边缘锯齿没有关系,你完全可以把两道痕迹当作没有粗细之分的理想曲线;为了解决这个问题,必须仔细分析自行车驶过后两道车轮印一定会满足的几何性质。
答案:自行车只有前车轮可以自由改变方向,后车轮的方向始终指向前车轮的中心。也就是说,如果把前后车轮的痕迹分别记为曲线 A 和曲线 B ,第 t 时刻前车轮的位置记为 A(t) ,后车轮的位置记为 B(t) ,则对任意时刻 t , A(t) 和 B(t) 的连线都与曲线 B 相切,且这条连线的长度是一个定值(两车轮间的距离)。换个角度来说,曲线 B 上任意一点的(其中一个方向上的)切线一定会与曲线 A 产生交点,且两个点的距离是一个定值。
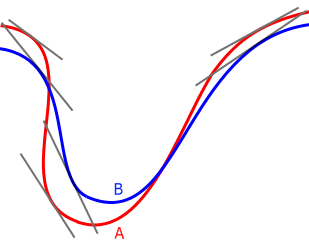

图2
由于曲线 B 的切线一定与另一条曲线相交,作出两条曲线各个部分上的切线,我们就可以区别出两道车轮印哪条是前轮痕迹 A ,哪条是后轮痕迹 B 。
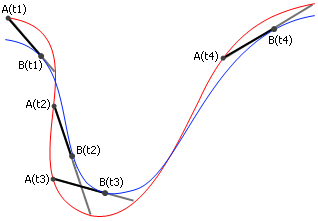

图3
下面在曲线 B 上任意取几个点,比如 B(t1) 、 B(t2) 、 B(t3) 、 B(t4) ,我们只需要找出对应的 A(t1) 、 A(t2) 、 A(t3) 、 A(t4) 的位置,即可还原出自行车行驶的大致过程了。由于 A(t) 一定在曲线 B 过 B(t) 点的切线上,作出各个 B(t) 的切线,它与曲线 A 的交点就应该是各个 A(t) 的位置。但这些切线与曲线 A 都有两个交点,哪个才是真正的 A(t) 呢?利用 A(t) 与 B(t) 间的距离为定值这一结论,我们可以看出,只有位于各 B(t) 左边的那些交点才与 B(t) 保持相同的距离。因此,自行车是从右往左行驶的。
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











