2014年韩国首尔举行国际数学家大会ICM(http://www.icm2014.org/)中,组委会曾制作了一套数学主题的台历,里面使用数学内容与日历的每一天都相映成趣。【遇见数学】会按今年日期每天发布这个旧台历上相应的内容。
— 2018.3.5 —

图1
一、正多面体只有 5 个
正多面体,或称柏拉图立体,指各面都是全等的正多边形且每一个顶点所接的面数都是一样的凸多面体。
判断正多面体的依据有三条:
正多面体的面由正多边形构成;
正多面体的各个顶角相等;
正多面体的各条棱边都相等。
这三个条件都必须同时满足,否则就不是正多面体。
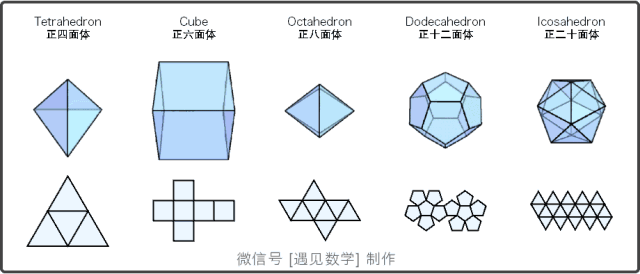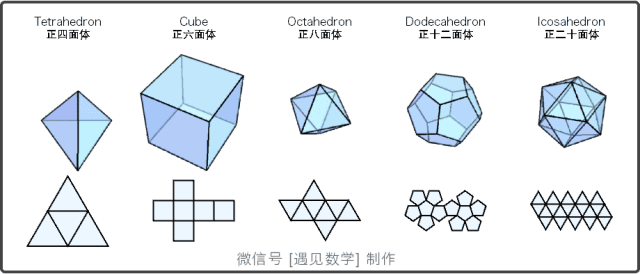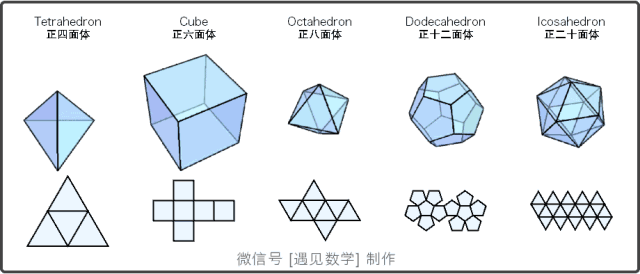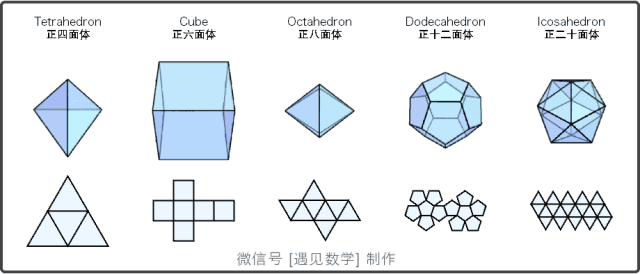
图2:正多面体以及展开平面图
正多面体的别称柏拉图立体是因柏拉图而命名的。柏拉图的朋友泰阿泰德告诉柏拉图这些立体,柏拉图便将这些立体写在《蒂迈欧篇》(Timaeus)内。正多面体的作法收录《几何原本》的第13卷。在命题13描述正四面体的作法;命题14为正八面体作法;命题15为立方体作法;命题16则是正二十面体作法;命题17则是正十二面体作法。
二、象征意义
柏拉图视“四古典元素”为元素,其形状如正多面体中的其中四个。
火的热令人感到尖锐和刺痛,好像小小的正四面体。
空气是用正八面体制的,可以粗略感受到,它极细小的结合体十分顺滑。
当水放到人的手上,它会自然流出,那它就应该是由很多小球所组成,好像正二十面体。
土与其他的元素相异,因为它可以被堆叠,正如立方体。
剩下没有用的正多面体——正十二面体,柏拉图以不清晰的语调写:“神使用正十二面体以整理整个天空的星座。”柏拉图的学生亚里士多德添加了第五个元素——以太,并认为天空是用此组成,但他没有将以太和正十二面体连系。
约翰内斯·开普勒依随文艺复兴建立数学对应的传统,将五个正多面体对应五个行星——水星、金星、火星、木星和土星,同时它们本身亦对应了五个古典元素。
三、用途
因为正多面体的形状的骰子会较公平,所以正多面体骰子经常出现于角色扮演游戏。

图3:一组正多面体骰子
正四面体、立方体和正八面体,亦会自然出现于结晶体的结构。
正多面体经过削角操作可以得到其他对称性类似的结构,比如著名的球状分子碳六十空间结构就是正二十面体经过削角操作得到的,称为截角二十面体。因此可以知道,碳六十分子所属的对称性群也是与正二十面体相同的Ih群。
由于正多面体和由正多面体衍生的削角正多面体大多有很好的空间堆积性质,即可以在空间中紧密堆积,因此常常选择正多面体形或者削角正多面体形的盒子作为分子模拟计算的周期边界条件。
参考资料:中文维基
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











