图1
欧拉公式将指数函数的定义域扩大到了复数域，建立和三角函数和指数函数的关系，被誉为“数学中的天桥”。形式简单，结果惊人，欧拉本人都把这个公式刻在皇家科学院的大门上，看来必须好好推敲一番。
一、复数
在进入欧拉公式之前，我们先看一些重要的复数概念。
1. 
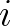的由来
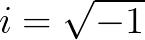，这个就是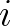的定义。虚数的出现，把实数数系进一步扩张，扩张到了复平面。实数轴已经被自然数、整数、有理数、无理数塞满了，虚数只好向二维要空间了。
可是，这是最不能让人接受的一次数系扩张，听它的名字就感觉它是“虚”的：
从自然数扩张到整数： 增加的负数可以对应“欠债、减少”
从整数扩张到有理数： 增加的分数可以对应“分割、部分”
从有理数扩张到实数： 增加的无理数可以对应“单位正方形的对角线的长度(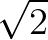
)”
从实数扩张到复数： 增加的虚数对应什么？
虚数似乎只是让开方运算在整个复数域封闭了（即复数开方运算之后得到的仍然是复数）。
看起来我们没有必要去理会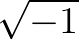
到底等于多少，我们规定
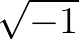没有意义就可以了嘛，就好像
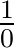一样。
我们来看一下，一元二次方程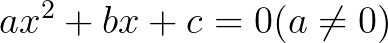
的万能公式：其根可以表示为：
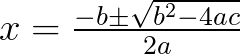，其判别式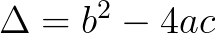
。
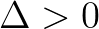：有两个不等的实数根
：有两个相等的实数根
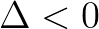：有两个不同的复数根，其实规定为无意义就好了，干嘛理会这种情况？
我们再看一下，一元三次方程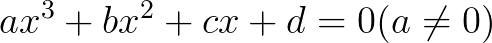
，一元三次方程的解太复杂了，这里写不下，大家可以参考维基百科，但愿大家能够打开。
我们讨论一下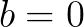
，此时，一元三次方程可以化为
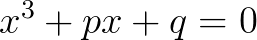，其根可以表示为：
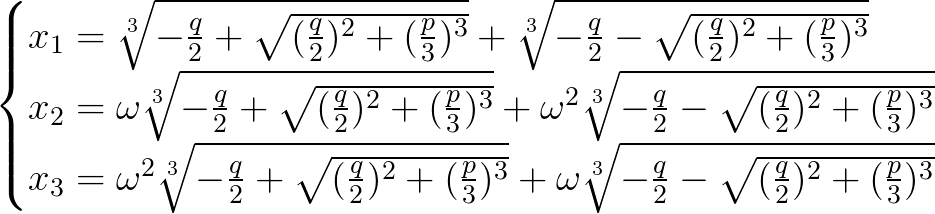
其中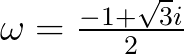
。
判别式为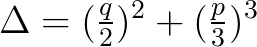
，注意观察解的形式，
是被包含在根式里面的。
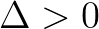：有一个实数根和两个复数根
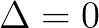：有三个实数根，当
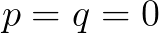，根为0，当
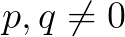，三个根里面有两个相等
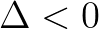：有三个不等的实根！懵了，要通过复数才能求得实根？
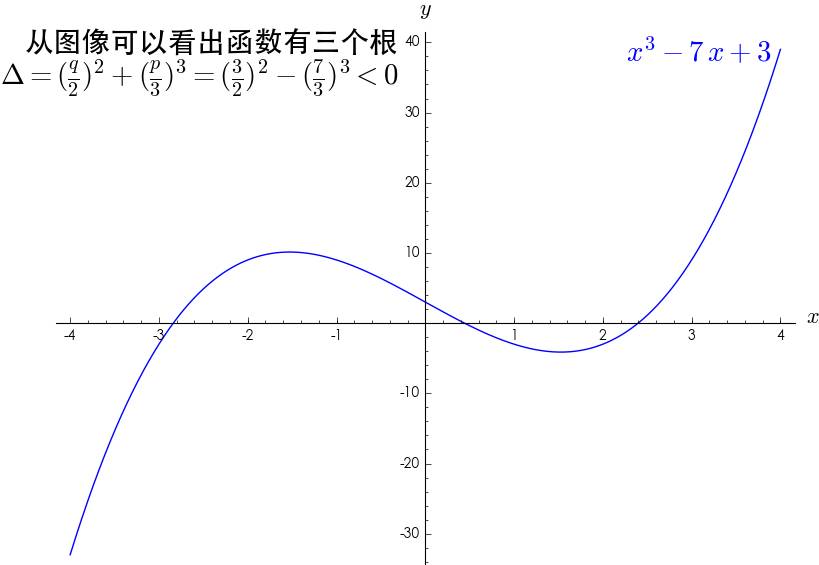
图2
要想求解三次方程的根，就绕不开复数了吗？后来虽然发现可以在判别式为负的时候通过三角函数计算得到实根，但是在当时并不知道，所以开始思考复数到底是什么？
我们认为虚数可有可无，虚数却实力刷了存在感。虚数确实没有现实的对应物，只在形式上被定义，但又必不可少。数学界慢慢接受了复数的存在，并且成为重要的分支。
2. 复平面上的单位圆
在复平面上画一个单位圆，单位圆上的点可以用三角函数来表示：
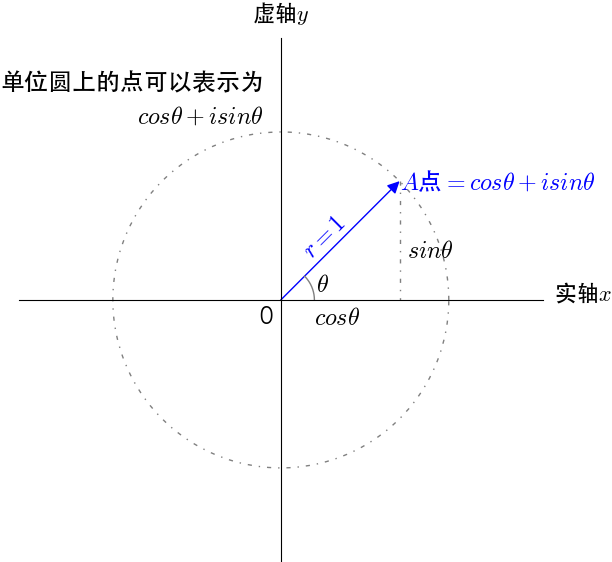
图3
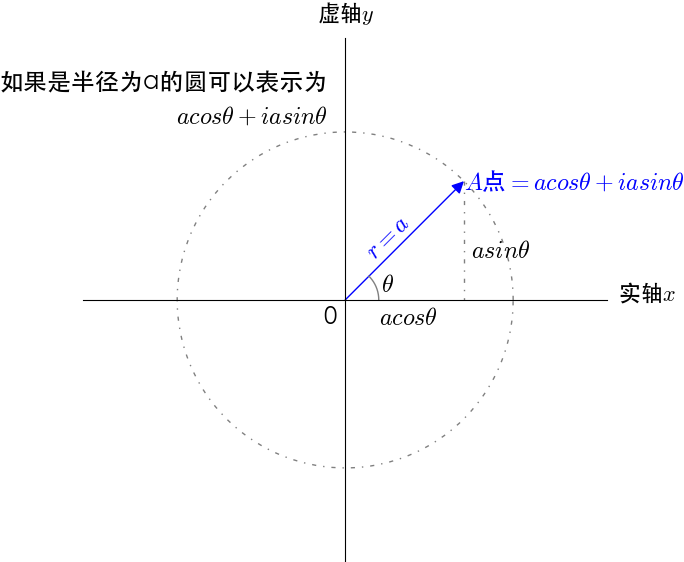
图4
我们来动手玩玩单位圆：
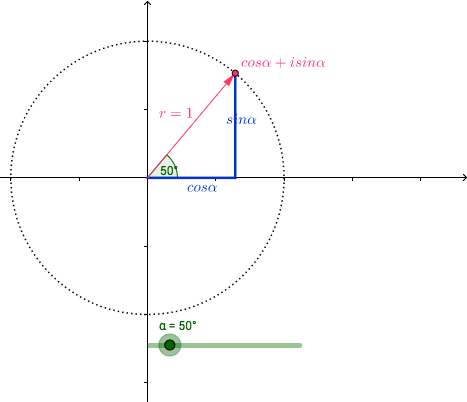
图5（此处有互动内容，点击最下面的“阅读原文”进行操作。需要流量较大，最好有wifi处打开，土豪请随意。）
3. 复平面上乘法的几何意义
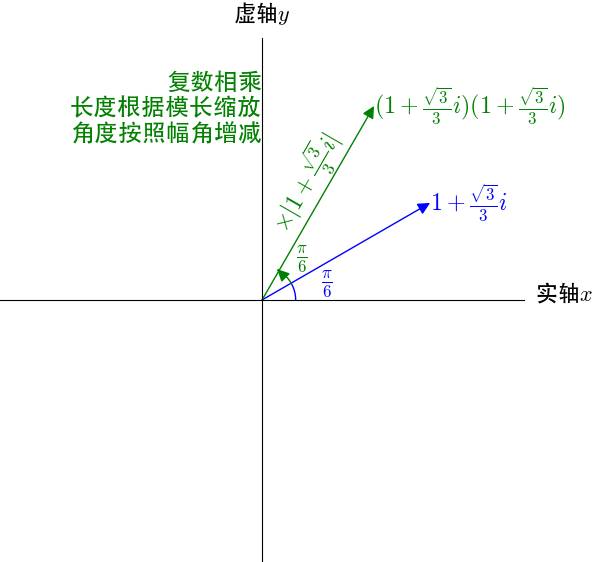
图6
同样来感受一下：
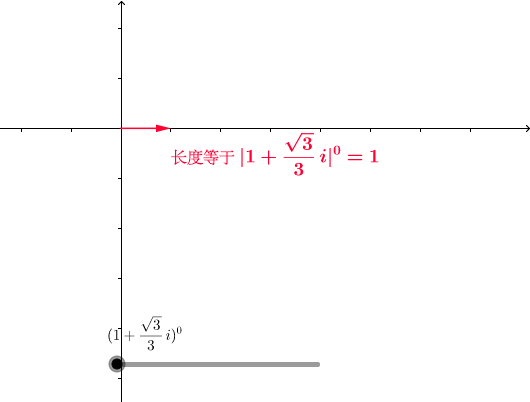
图7（此处有互动内容，点击最下面的“阅读原文”进行操作。需要流量较大，最好有wifi处打开，土豪请随意。）
二、欧拉公式
对于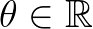
，有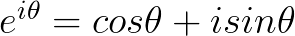
。
----维基百科
欧拉公式在形式上很简单，是怎么发现的呢？
1. 欧拉公式与泰勒公式
欧拉最早是通过泰勒公式观察出欧拉公式的：
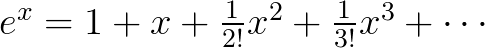
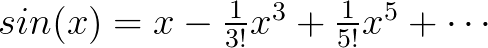
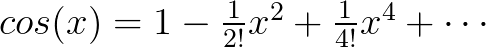
将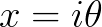
代入
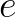可得：
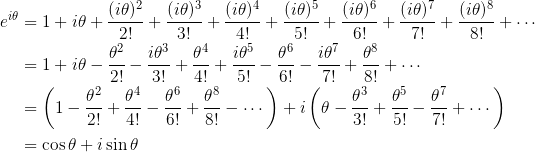
那欧拉公式怎么可以有一个直观的理解呢？
2. 对同一个点不同的描述方式
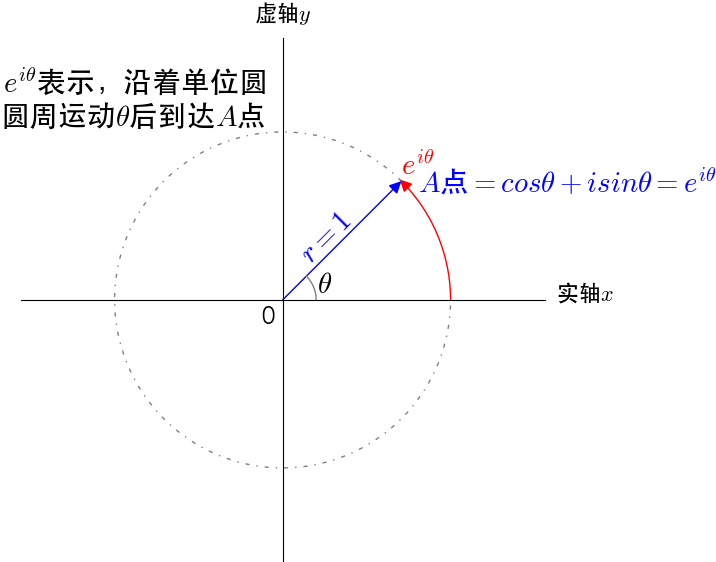
图8
我们可以把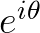
看作通过单位圆的圆周运动来描述单位圆上的点，
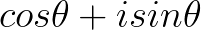通过复平面的坐标来描述单位圆上的点，是同一个点不同的描述方式，所以有
。
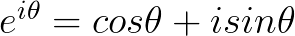3. 为什么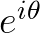
是圆周运动？
定义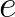
为：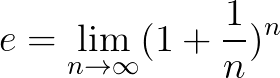 
----维基百科
这是实数域上的定义，可以推广到复数域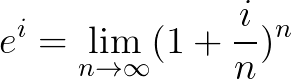
。根据之前对复数乘法的描述，乘上
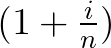是进行伸缩和旋转运动，
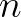取值不同，伸缩和旋转的幅度不同。
我们来看看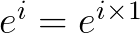
如何在圆周上完成1弧度的圆周运动的：
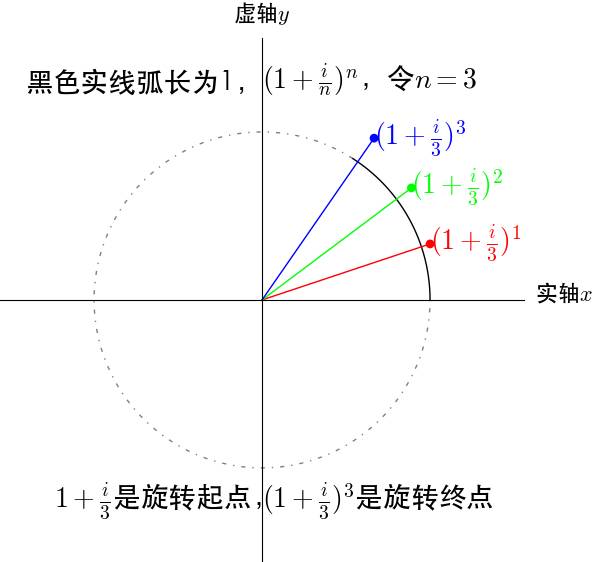
图9
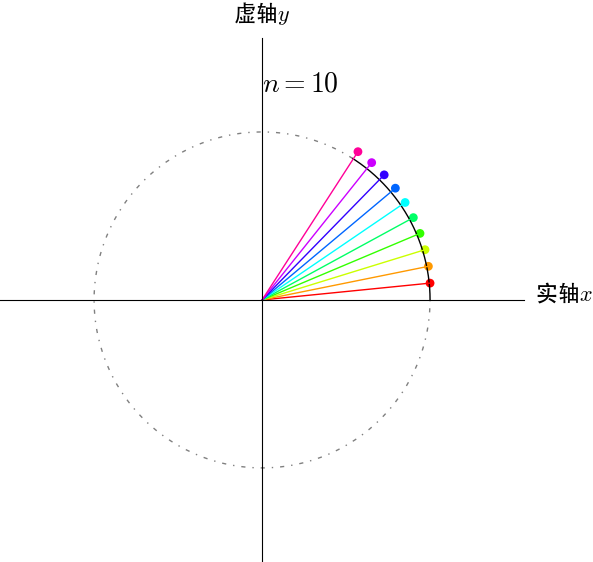
图10
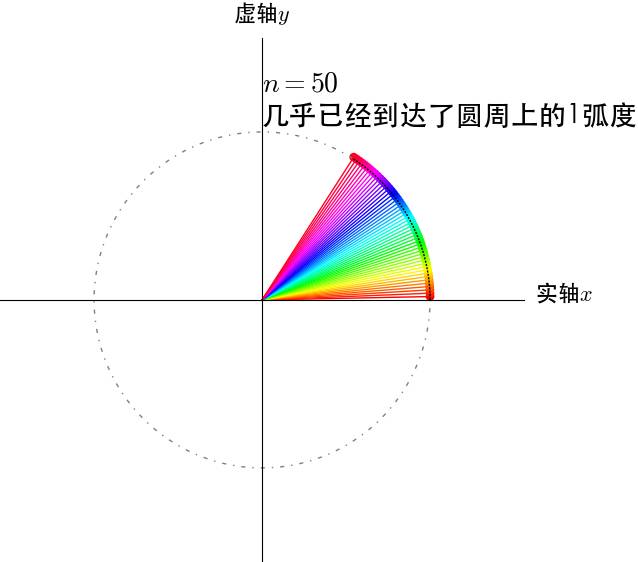
图11
从图上可以推出
时，
在单位圆上转动了1弧度。
再来看看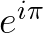
，这个应该是在单位圆上转动
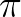弧度：
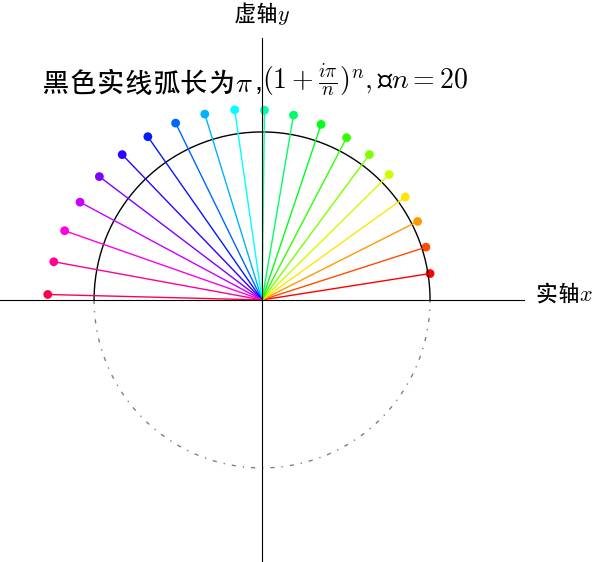
图12
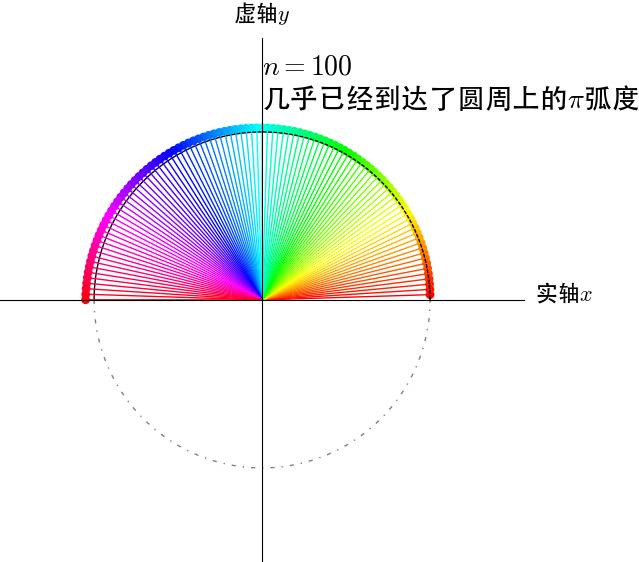
图13
看来
确实是单位圆周上的圆周运动。
动手来看看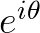
是如何运动的吧：
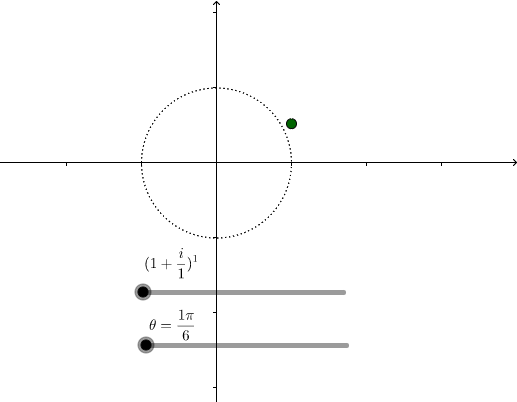
图14（此处有互动内容，点击最下面的“阅读原文”进行操作。需要流量较大，最好有wifi处打开，土豪请随意。）
4. 
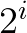的几何含义是什么？
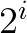看不出来有什么几何含义，不过我们稍微做个变换
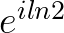，几何含义还是挺明显的，沿圆周运动
弧度。
5. 欧拉公式与三角函数
根据欧拉公式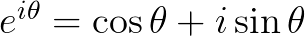
，可以轻易推出：
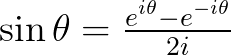和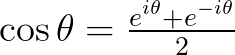 
。三角函数定义域被扩大到了复数域。
我们把复数当作向量来看待，复数的实部是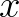
方向，虚部是
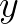方向，很容易观察出其几何意义。
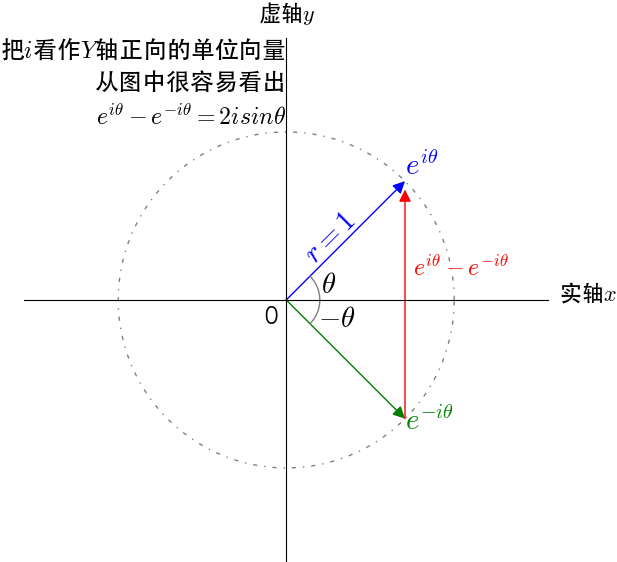
图15
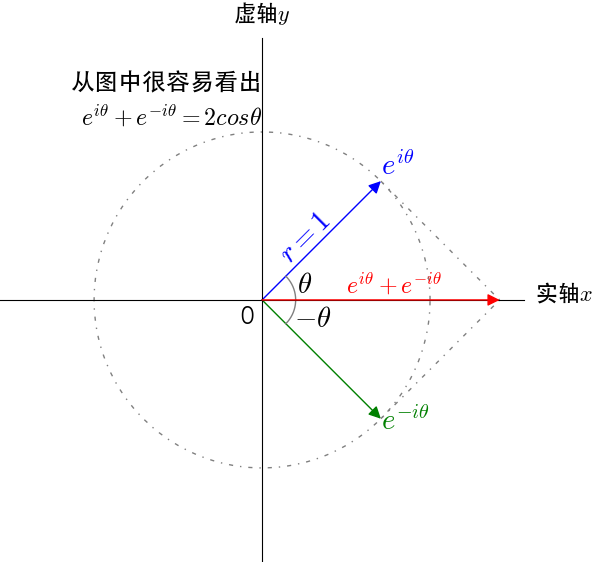
图16
6. 欧拉恒等式
当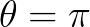
的时候，代入欧拉公式：
。
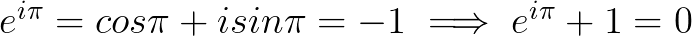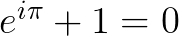就是欧拉恒等式，被誉为上帝公式，
、
、
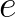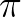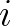、乘法单位元1、加法单位元0，这五个重要的数学元素全部被包含在内，在数学爱好者眼里，仿佛一行诗道尽了数学的美好。
声明：文章转自【马同学高等数学】微信公众号，版权归原作者所有，转载仅供学习使用，不用于任何商业用途，如有侵权请联系删除，谢谢。
