此前在另外一篇文章尝试给对傅立叶级数、傅立叶变换进行过稍微直观点的解释。本文会对公式进行细节的、代数上的解释。
一、对周期函数进行分解的猜想
拉格朗日等数学家发现某些周期函数可以由三角函数的和来表示，比如下图中，黑色的斜线就是周期为
的函数，而红色的曲线是三角函数之和，可以看出两者确实近似：
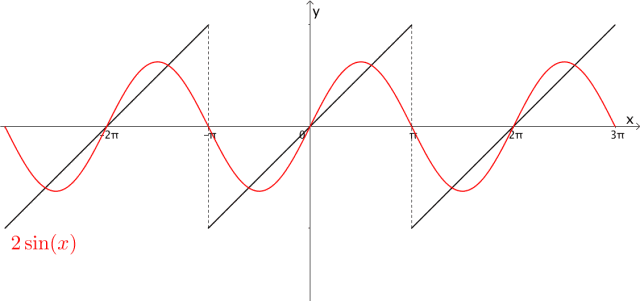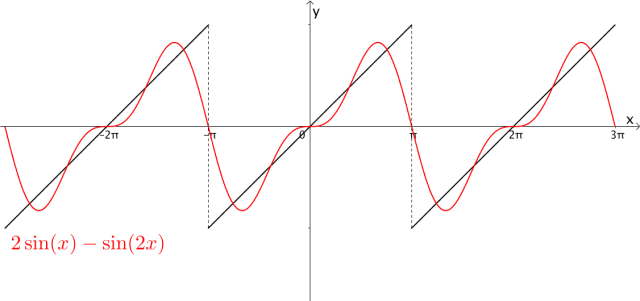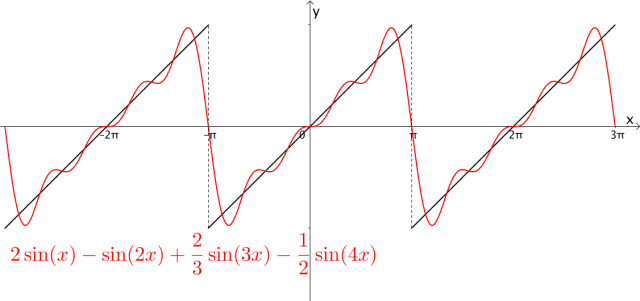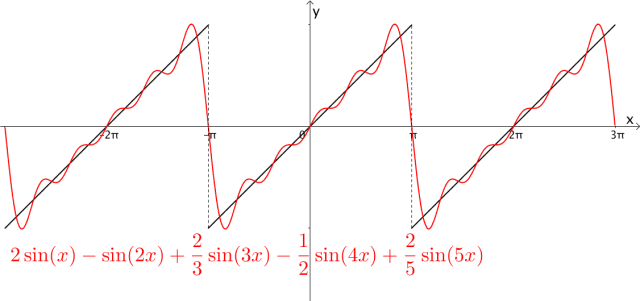
图1
而另外一位数学家：
图2
让·巴普蒂斯·约瑟夫·傅里叶男爵(1768-1830)猜测任意周期函数都可以写成三角函数之和。
二、分解的思路
假设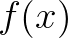
是周期为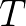
的函数，傅里叶男爵会怎么构造三角函数的和，使之等于
？
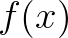1. 常数项
对于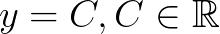
这样的常数函数：
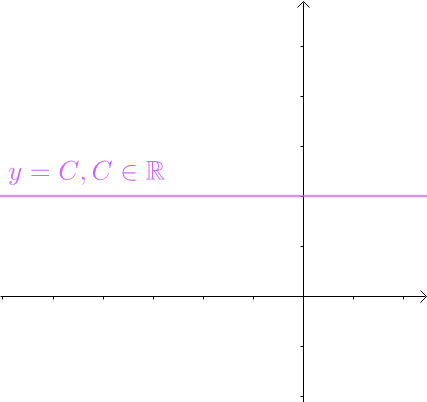
图3
根据周期函数的定义，常数函数是周期函数，周期为任意实数。
所以，分解里面得有一个常数项。
2. 通过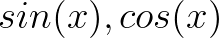
进行分解
首先，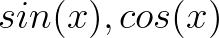
是周期函数，进行合理的加减组合，结果可以是周期函数。
其次，它们的微分和积分都很简单。
然后，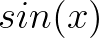
是奇函数，即：
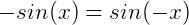
从图像上也可以看出，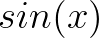
关于原点对称，是奇函数：
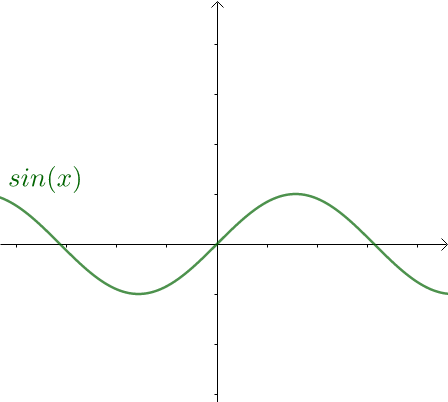
图4
而奇函数与奇函数加减只能得到奇函数，即：
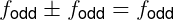
其中，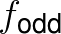
表示奇函数。
而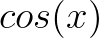
是偶函数，即：
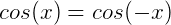
从图像上也可以看出，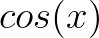
关于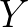
轴对称，是偶函数：
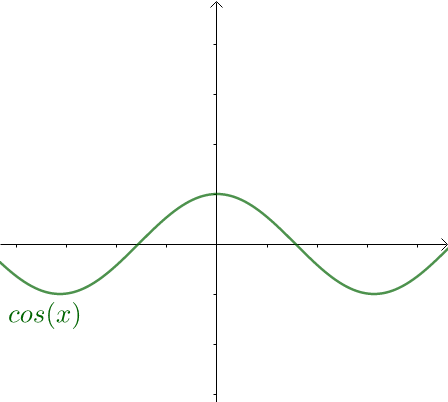
图5
同样的，偶函数与偶函数加减只能得到偶函数，即：
其中，
表示偶函数。
但是任意函数可以分解和奇偶函数之和：
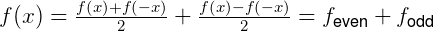
所以同时需要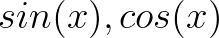
。
3. 保证组合出来周期为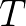
之前说了，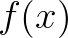
是周期为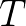
的函数，我们怎么保证组合出来的函数周期依然为
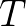呢？
比如下面这个函数的周期为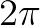
：
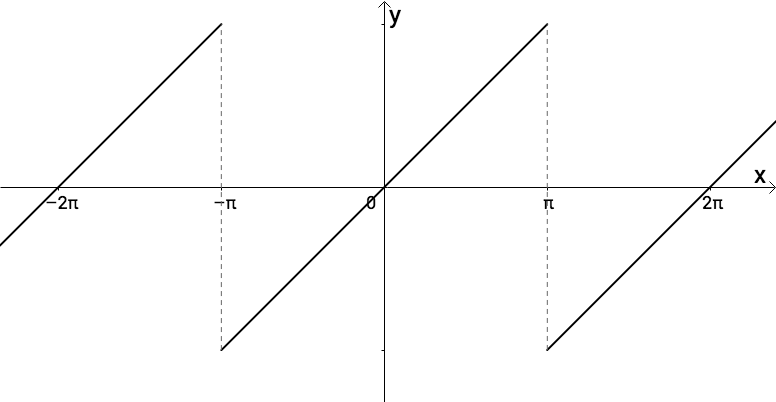
图6
很显然，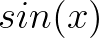
的周期也是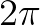
：
图7
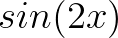的周期也是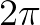
，虽然最小周期是
：
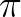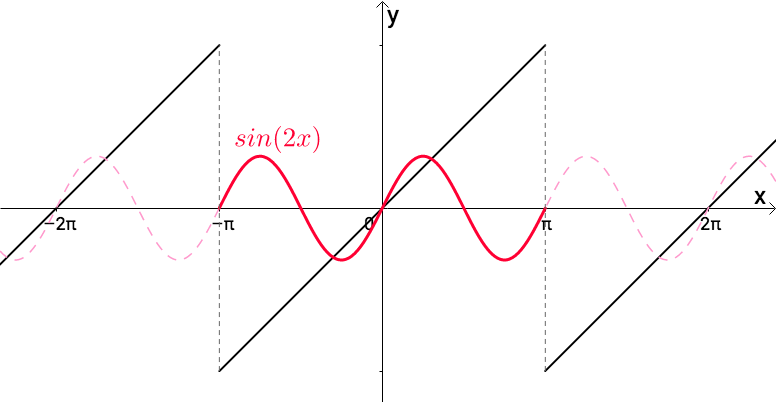
图8
很显然，
的周期都是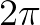
：
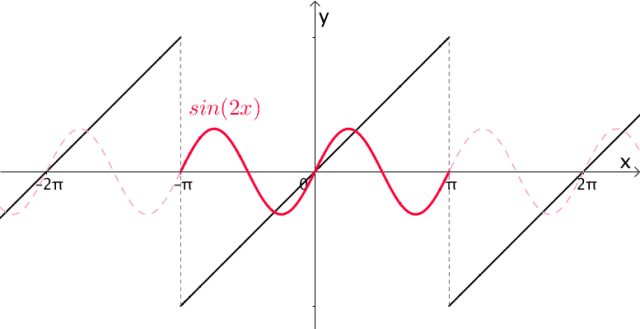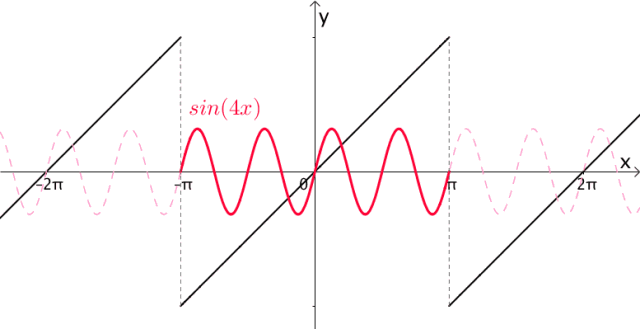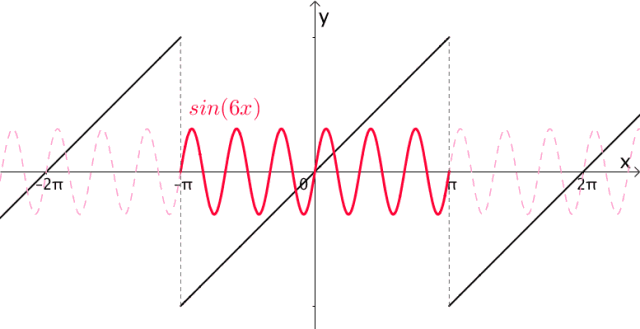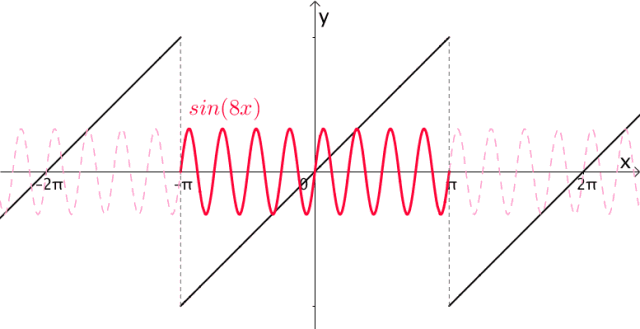
图9
更一般的，如果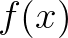
的周期为
，那么：
这些函数的周期都为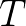
。
将这些函数进行加减，就保证了得到的函数的周期也为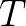
。
4. 调整振幅
现在我们有一堆周期为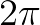
的函数了，比如说
：
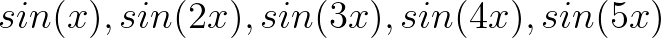图10
通过调整振幅可以让它们慢慢接近目标函数，比如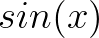
看起来处处都比目标函数低一些：
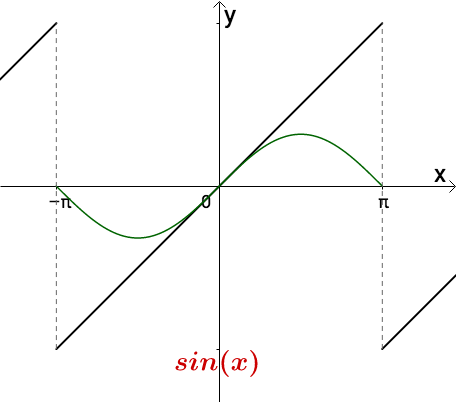
图11
把它的振幅增加一倍：
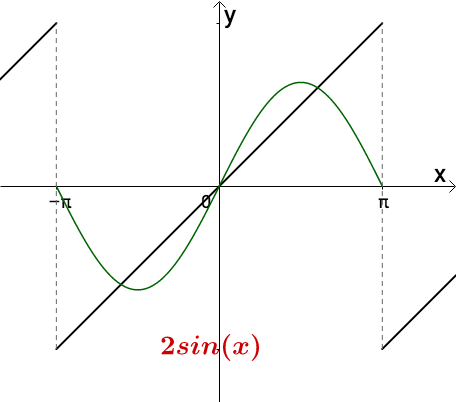
图12
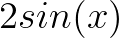有的地方超出去了，从周期为
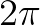的函数中选择一个，减去一点：
图13
调整振幅，加加减减，我们可以慢慢接近目标函数：
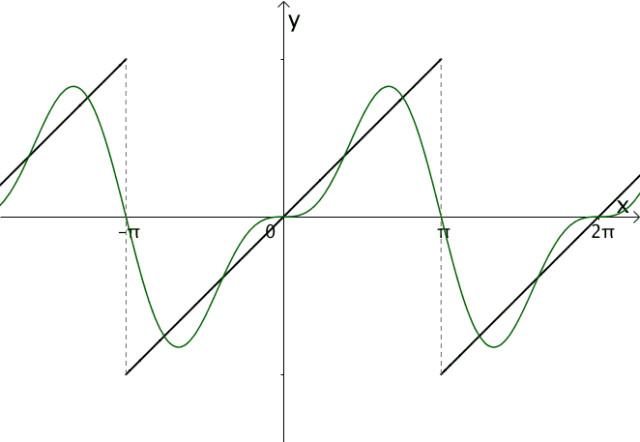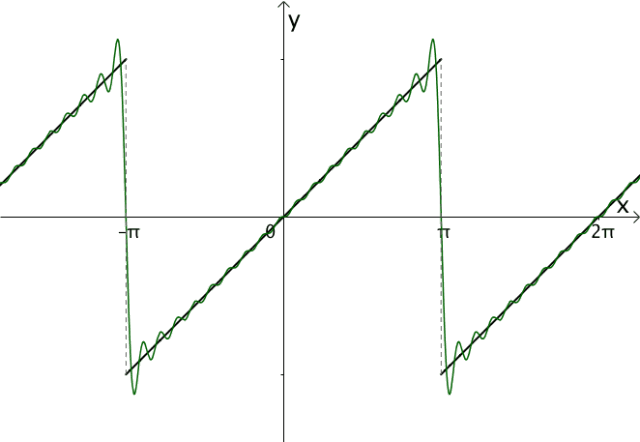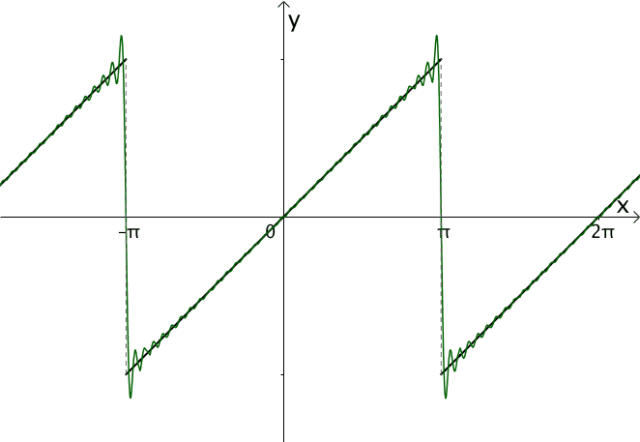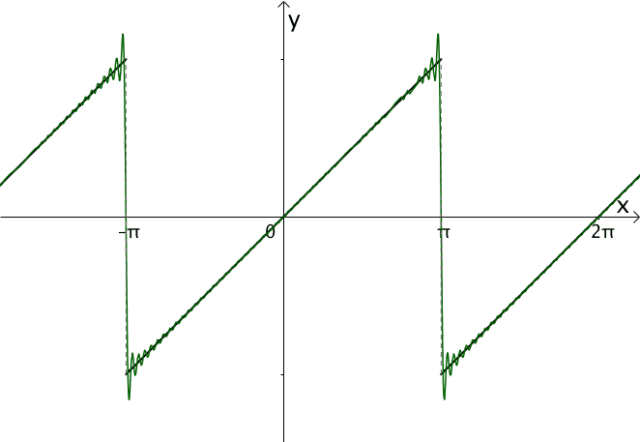
图14
5. 小结
综上，构造出来的三角函数之和大概类似下面的样子：
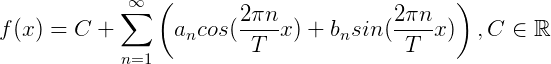
这样就符合之前的分析：
● 有常数项
● 奇函数和偶函数可以组合出任意函数
●周期为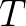
● 调整振幅，逼近原函数
之前的分析还比较简单，后面开始有点难度了。即怎么确定这三个系数：
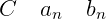
三、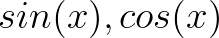
的另外一种表示方法
直接不好确定，要迂回一下，先稍微介绍一下什么是：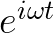
？
1. 
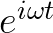
看到复数也不要怕，根据之前的文章如何通俗易懂地解释欧拉公式，看到类似于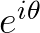
这种就应该想到复平面上的一个夹角为
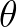的向量：
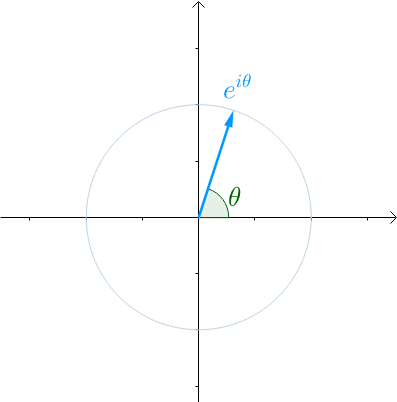
图15
那么当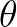
不再是常数，而是代表时间的变量
的时候：
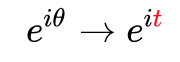
随着时间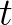
的流逝，从0开始增长，这个向量就会旋转起来，
秒会旋转一圈，也就是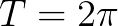
：
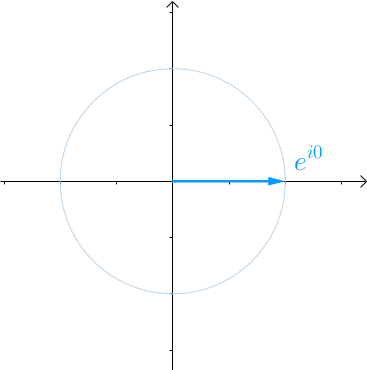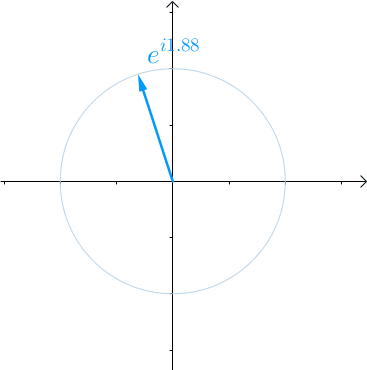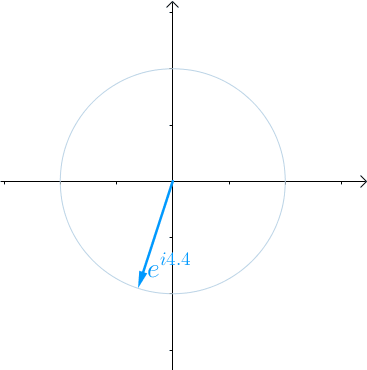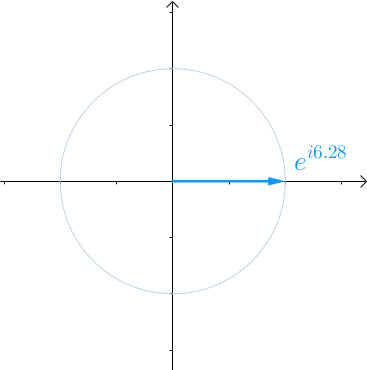
图16
2. 通过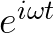
表示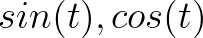 
根据欧拉公式，有：
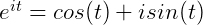
所以，在时间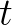
轴上，把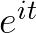
向量的虚部（也就是纵坐标）记录下来，得到的就是
：
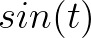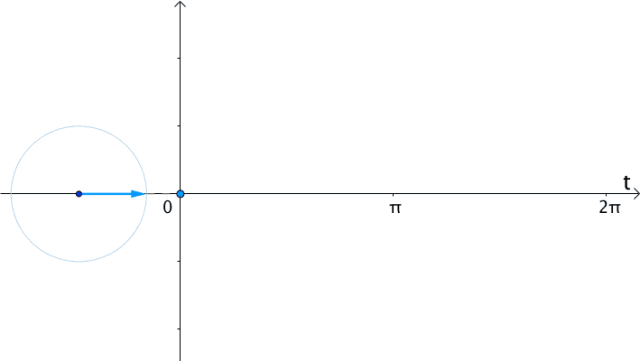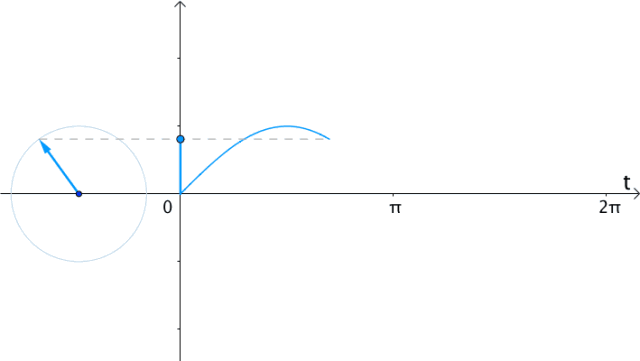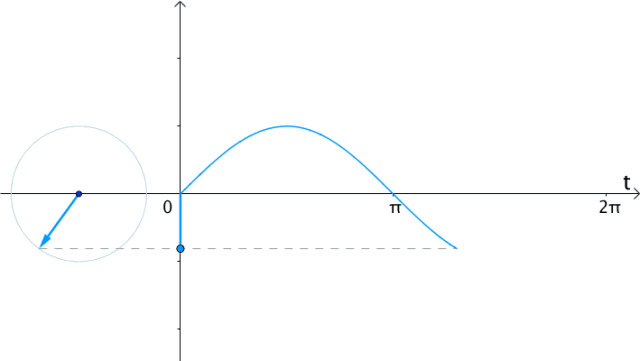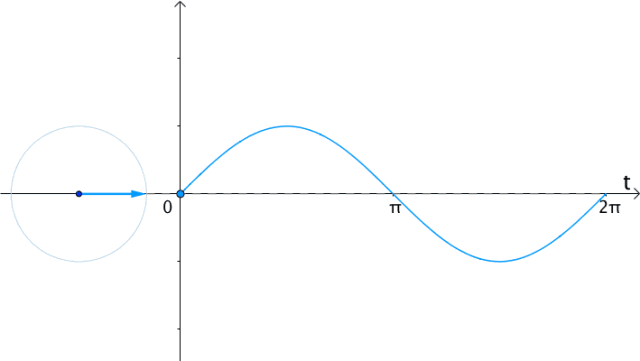
图17
代数上用
表示虚部：
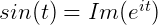
在时间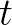
轴上，把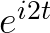
向量的虚部记录下来，得到的就是
：
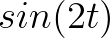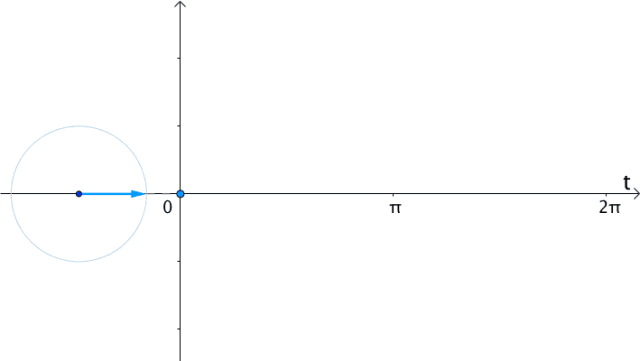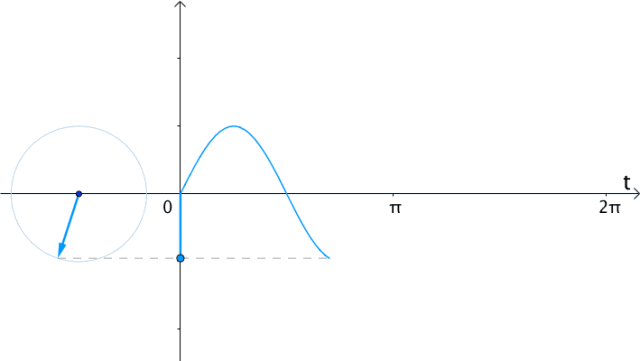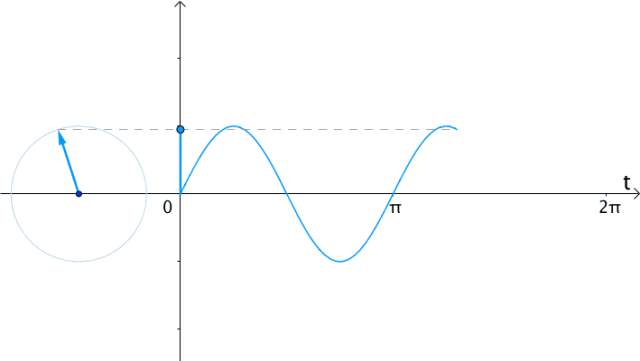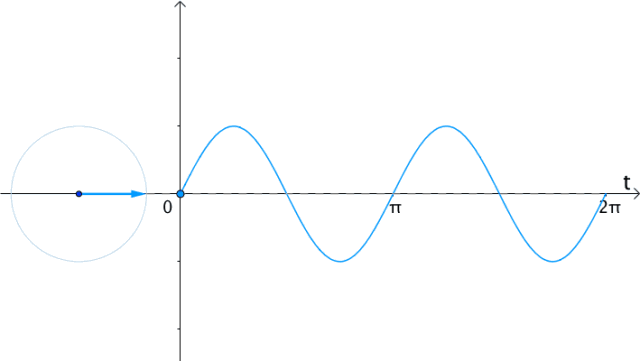
图18
如果在时间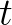
轴上，把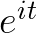
的实部（横坐标）记录下来，得到的就是
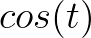的曲线：
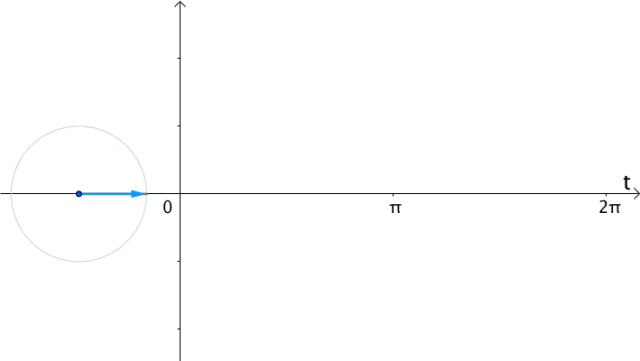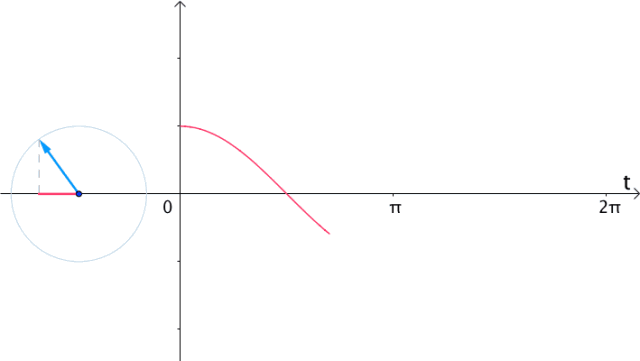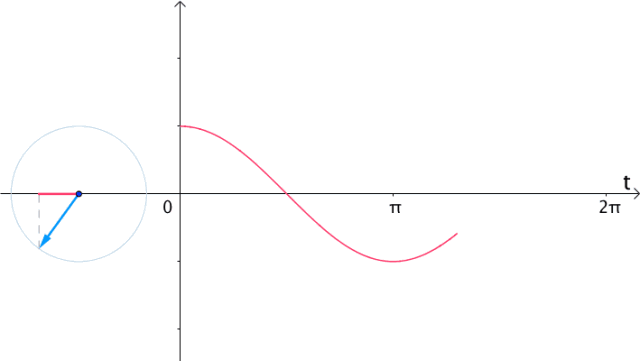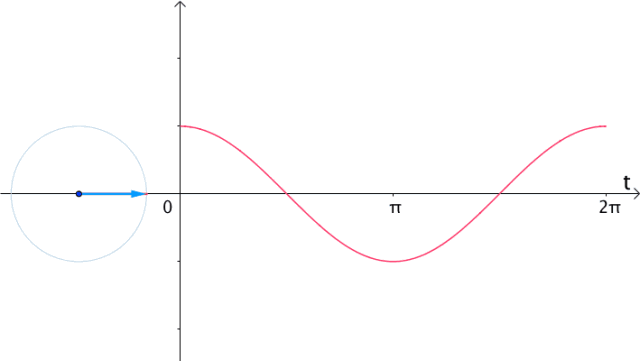
图19
代数上用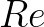
表示实部：
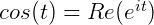
在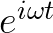
的图像中，可以观察到旋转的频率，所以称为频域；而在
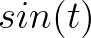中可以看到流逝的时间，所以称为时域：
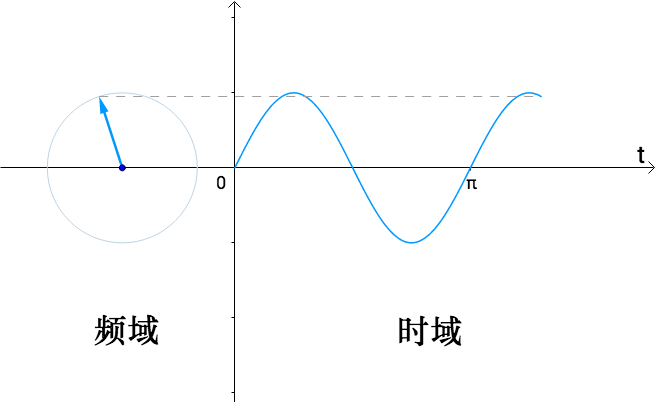
图20
四、通过频域来求系数
1. 函数是线性组合
假设有这么个函数：
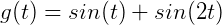
是一个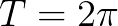
的函数：
图21
如果转到频域去，那么它们是下面这个复数函数的虚部：
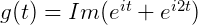
先看看
，其中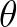
是常数，很显然这是两个向量之和：
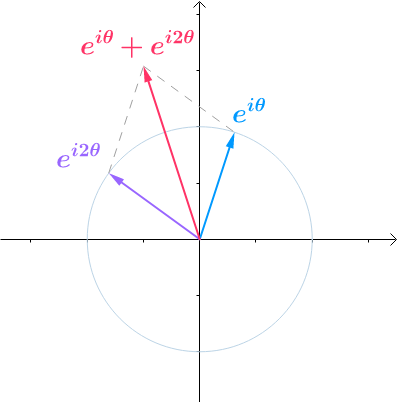
图22
现在让它们动起来，把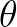
变成流逝的时间
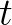，那么就变成了旋转的向量和：
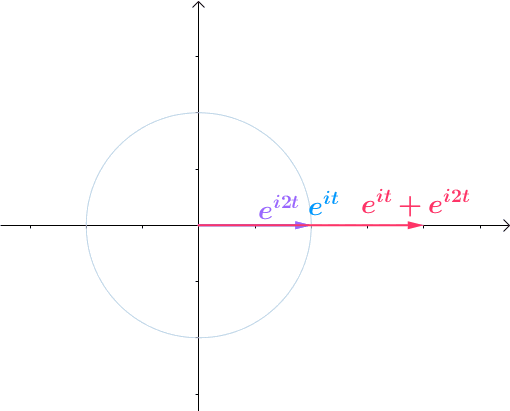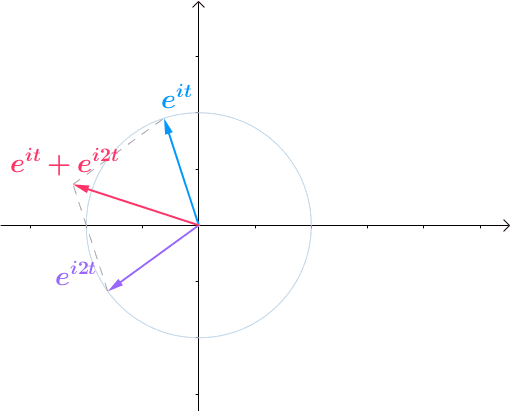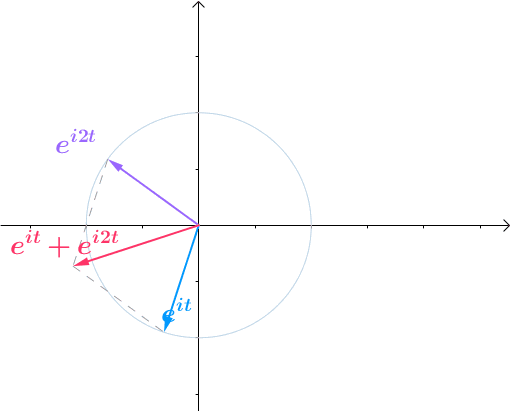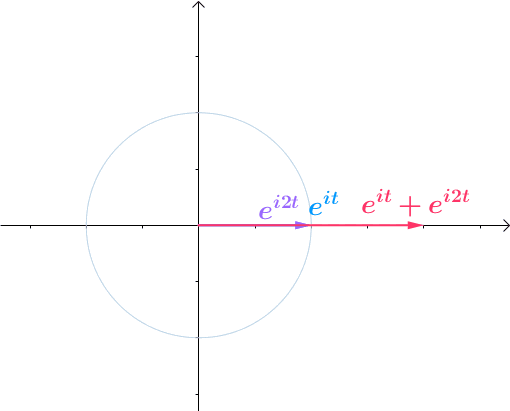
图23
很显然，如果把虚部记录下来，就得到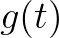
：
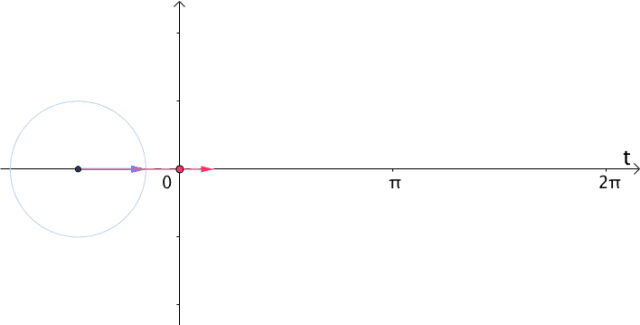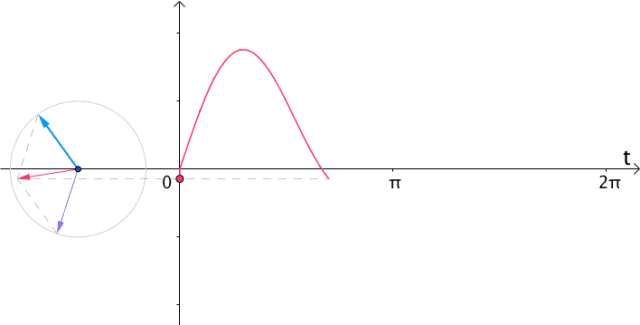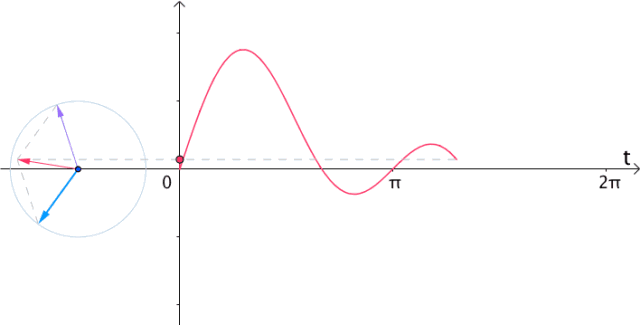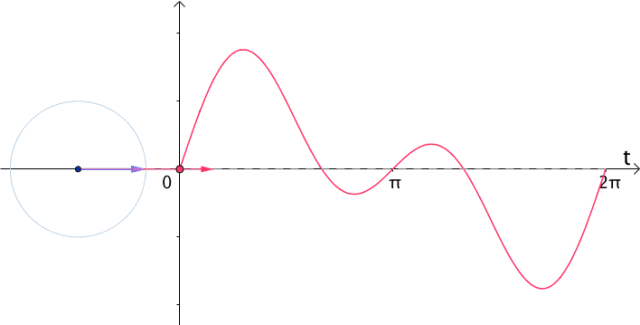
图24
2. 函数向量
前面画了一大堆图，就想说明一个观点，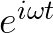
是向量，并且是旋转的向量。
而根据欧拉公式，有：
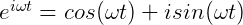
从图像上看：
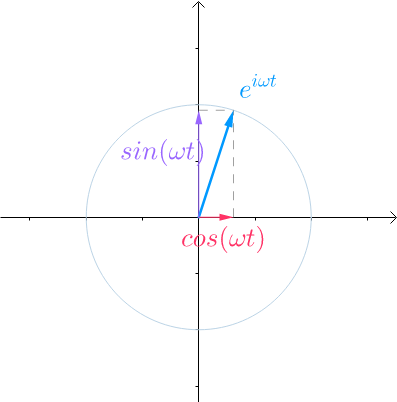
图25
所以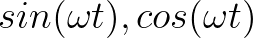
也是向量。
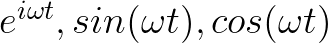称为函数向量，并且函数向量的点积是这么定义的：
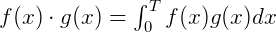
其中，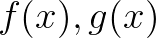
是函数向量，
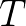是
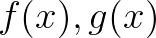的周期。
关于函数向量，关于函数向量的点积，更严格的讨论可以参考无限维的希尔伯特空间。
3. 
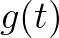是线性组合
虽然比较仓促，让我们先接受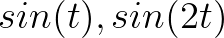
是函数向量，那么它们的线性组合得到的也是函数向量：
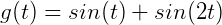
根据刚才的点积的定义有：
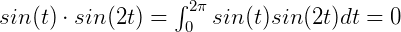
根据点积的代数和几何意义（关于点积的几何意义可以参考这篇文章），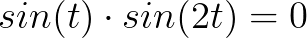
说明了，这两个函数向量正交、线性无关，是正交基。
如果写成这样：
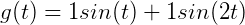
可以理解为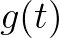
在正交基
下的坐标为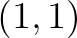
。
4. 如何求正交基的坐标
我们来看个例子，假设：
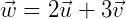
其中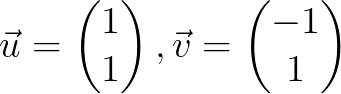
通过点积：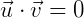
可知这两个向量正交，是正交基。图示如下：
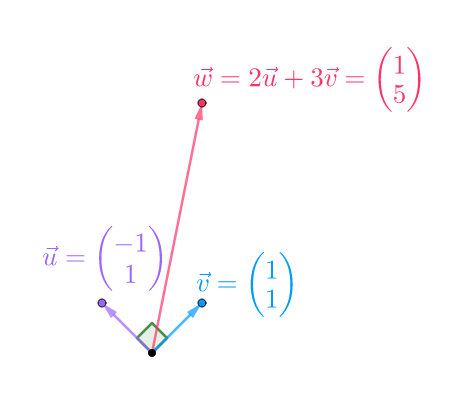
图26
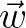在基
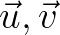下的坐标为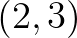
，其中在基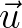
下的坐标可以通过点积这么来算（对于正交基才可以这么做）：
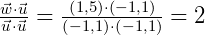
5. 如何求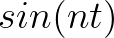
基下的坐标
对于：
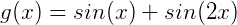
其中，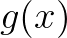
是向量，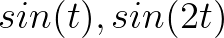
是正交基，周期
。
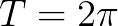所以是正交基，那么根据刚才的分析，可以这么求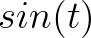坐标
上的坐标：
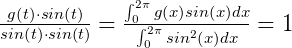
6. 更一般的
对于我们之前的假设，其中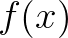
周期为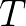
：
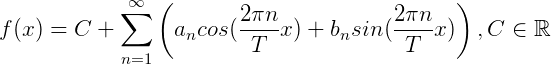
可以改写为这样：
也就是说向量
是以下正交基的线性组合：
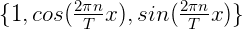
是的，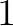
也是基。
那么可以得到：
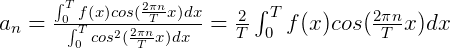
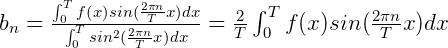
也可以通过点积来表示，最终我们得到：
其中：
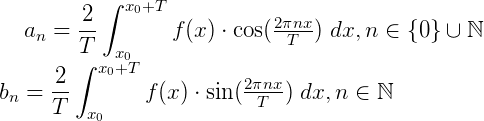
五、傅立叶级数的另外一种表现形式
根据欧拉公式：
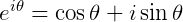
我们可以推出：
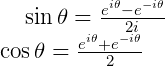
根据上式，我们可以写出傅立叶级数的另外一种形式：
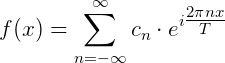
其中：
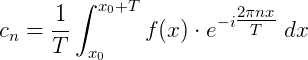
解读一下：
对于复数函数，定义的点积为：
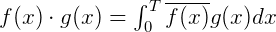
其中，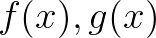
为复数函数，
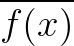是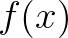
的共轭，所以
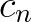的代数表达式中有一个负号。
顺便说一下，这样定义点积是为了保证：
声明：文章转自【马同学高等数学】微信公众号，版权归原作者所有，转载仅供学习使用，不用于任何商业用途，如有侵权请联系删除，谢谢。
