递归思想是一个自然界运行法则
一、汉诺塔
古印度神话故事中,在大梵天创造世界的时候,为了考验人类,做了三根金刚石柱子,在其中一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。
大梵天便命令教徒把圆盘按大小顺序重新摆放在另一根柱子上,但他还规定了一个规则:在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
大梵天对教徒们预言:当你们完成移动的那一刻,就是这个世界终结的时候。
1883年,法国数学家Édouard Lucas有一次碰巧听到这个故事,无聊中的Lucas开始思考怎么玩,然而Lucas发现移动64层圆盘的过程非常繁杂,脑袋根本无法承载这么大的计算量,便尝试将问题进行简化:把6个圆盘从一个柱子移动到另外一个柱子,最少需要多少步可以完成?
Lucas也给这个问题取名为汉诺塔问题。
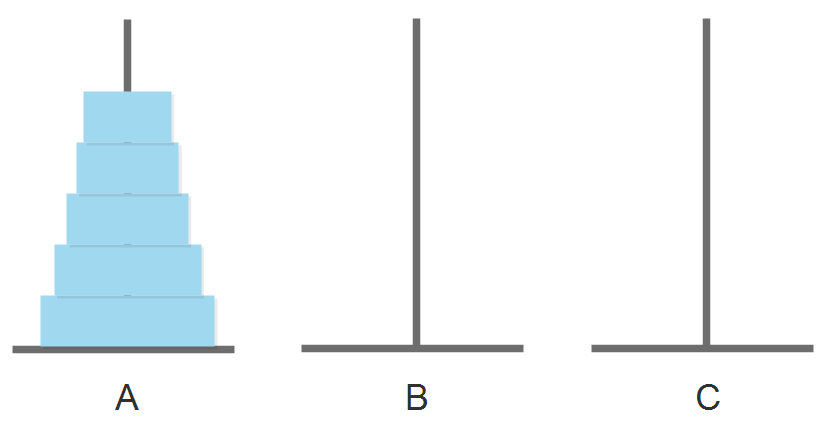
图1:汉诺塔问题示意图
其实对于汉诺塔问题,大家都应该很熟悉。不过为了计算更简便些,我们先尝试汉诺塔问题只有3个圆盘的情况下应该怎么做?这个估计大家在第一时间应该能够反应出来,最后发现只需7步就可以完成。

图2:3个圆盘的汉诺塔解法
当圆盘数量增加6个以后,这个时候可能就开始有点懵了:

图3:6个圆盘的汉诺塔解法
可以发现,随着圆盘数的增加,汉诺塔问题难度越来越大。不过人类最不怕的就是解决问题,针对汉诺塔问题,数学家们提出了一个非常巧妙解法,递归解法:
Step 1:将A柱子上的n-1个圆盘搬到B柱子上
Step 2:将A柱子上剩下的大圆盘搬到C柱子上
Step 3:将B柱子上的n-1个圆盘搬到C柱子上
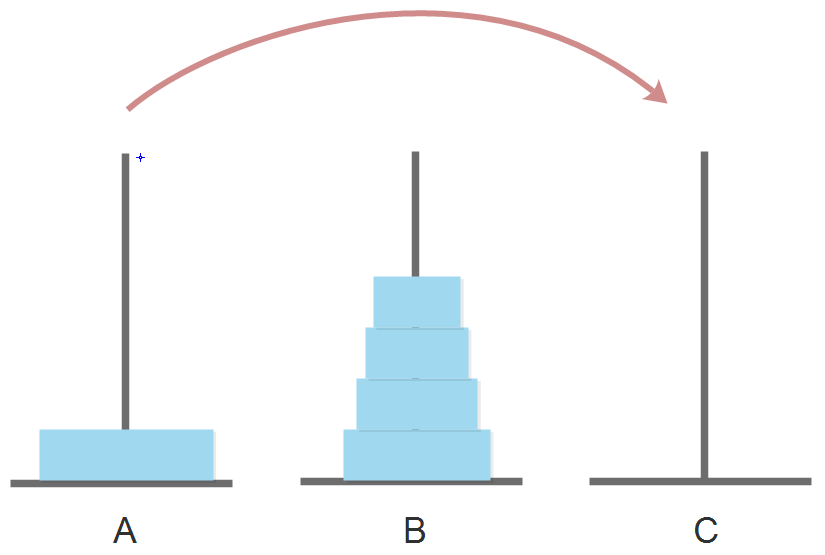
图4:递归解法的关键步骤:移动最大的圆盘到目的地
我们再考虑一下n-1个圆盘是怎么从A柱子搬到B柱子上的。我们可以重复上述的过程,完全跟搬从A柱子把n个圆盘搬到C柱子的过程类似。
Step 1:将A柱子上的n-2个圆盘搬到C柱子上
Step 2:将A柱子上第n-1个大圆盘搬到B柱子上
Step 3:将C柱子上的n-1个圆盘搬到B柱子上
移动的过程通过这种递归方式可以清晰描述出来,所以我们只需要从最顶层进行考虑。假设将n个圆盘从一个柱子全部搬到另外一个柱子上的最少移动次数是H(n),那么根据上面递归解法中的3步可以得到这个关系式:

这个递推表达式已经非常明确了,我们可以利用这个递推表达式,得到任意数量圆盘汉诺塔问题的最少移动步数。已知H(1)=1,进行一下推导以后我们得到:

代入算一下,H(3)=7,H(6)=63。而64层汉诺塔的最少移动次数是H(64)。假设移动1次需要1秒,需要5849亿年才能完成移动,远远大于当前宇宙年龄138亿年,吻合大梵天“预言”。估计大梵天早已洞悉这个问题的答案,靠人力来移动汉诺塔是一个不可能完成的任务,也就是说不可能世界末日。
一个看似复杂的问题,却蕴含着如此巧妙的递归解法,令人惊叹。汉诺塔在现代也成为了一款颇受欢迎的益智游戏,在娱乐过程中给人们传递着蕴含其中的递归思想。
二、递归的来源
20世纪50年代,在计算机诞生以后,Fortran是最早得到广的编程语言,Fortran源自于公式翻译的缩写(Formula Translation)。
Fortran是一个为计算而生的语言,但它的编译系统并未科学地解决一些主要的难题,其中一个就是程序不能调用自身。(尽管如此,Fortran语言一直在发展,最新版是Fortran 2018,在科学与工程界享有盛誉。)
1960年,荷兰计算机学家,艾兹格·W·迪杰斯拉克(Edsger Wybe Dijkstra)在他的著作《递归编程》(Recursive Programming)中首次明确描述可以在程序当中使用递归这个概念。
迪杰斯拉克遇到这么个问题,如果每个子程序(subroutine)在启动时都占据固定的工作空间,将导致两个后果。一是如果同时运行多个子程序,必将占用大量的空间,空间使用效率低。二是,若有一个子程序已经在运行,在这个子程序结束以前,不能再调用自己。因为调用自己时数据无法与上一次调用分隔开。
为了解决这种情况,迪杰斯拉克郑重地提出递归编程的概念(Recursive Programming)。
迪杰斯拉克独立发明了逆波兰记法(Reverse Polish notation,RPN),发展了栈(Stack)的概念,将栈的概念用于代码运行时的动态存储分配,实现递归调用子程序时的环境维护,在此基础上与荷兰程序员Jaap Zonneveld完成了ALGOL60的第一个版本,这是最早支持递归的高级语言。因为在ALGOL60上做出原理性贡献,Dijkstra获得了1972年的图灵奖(小智写过Dijkstra大神,感兴趣点击传送门)。

图5:图灵奖杯(图灵奖有计算机科学界诺贝尔奖之称)
逆波兰记法是什么?
逆波兰式将操作符号(operator)放在操作对象(operand)。我们可以用逆波兰记法试着转换一些简单的式子:
3 + 4 这个式子,可以表示为:3 4 +
3 - 4 + 5 这个式子,可以表示为:3 4 - 5 +
3 - 4 + 5 × 6 这个式子,可以表示为:3 4 - 5 6 × +
3 - (4 + 5) × 6 这个式子,可以表示为:3 4 5 + 6 × +
在逆波兰记法的作用下,在式子中不需要再使用括号来表示计算先后顺序。逆波兰记法极大帮助了计算机对式子计算过程的理解,而实现逆波兰记法需要借助栈。换句话说,栈实际上可以表示多个层次的程序运算,即实现递归。
从此,程序员们多了一个新词汇:递归。
三、什么是递归
递归(Recursion),是指在函数的定义中调用函数自身的方法。在数学与计算机科学中有非常重要的地位,也是众多公式与算法思想的源泉。
首先,最直观体现递归概念的公式是阶乘。n的阶乘,定义为1到n所有数的乘积。假设n的阶乘结果为F(n),我们可以将阶乘定义成下面这个式子:

其中F(1) = 1。
可以发现,n的阶乘可以用n-1的阶乘来进行定义,用自己的定义来定义自己,这就是递归的思想。
另外一个例子是斐波那契数列(Fibonacci sequence)。斐波那契(Fibonacci)是12世纪的意大利数学家。他在他的著作《算盘全书》(liber abaci)中记录了这样一个问题:
假设在围栏当中有一对刚出生的兔子(一只雄性,一只雌性)。这对兔子出生后的第二个月结束时开始可以生兔子,每个月可以生另外一对兔子(同样包含一只雄性,一只雌性,生育模式与父母相同)。再假设兔子不会死亡,一直可以生长下去。问一年内可繁殖成多少对兔子?
我们详细列一下每个月的情况:
第1个月,只有1对兔子
第2个月,还是1对兔子,还没开始生兔子
第3个月,新增1对兔子,加上第2个月的1对老兔子,一共2对兔子
第4个月,两个月前有1对兔子,可以生1对兔子,加上第3个月的2对兔子,一共有3对兔子
第5个月,两个月前有2对兔子,可以生2对兔子,加上第4个月的3对兔子,一共有5对兔子
……
所以,兔子生长序列可以写成下面这个数列:
1,1,2,3,5,8,13,……
可以发现,除了最前面的两个数字以外,其余的数字是前两个位置的数字之和。上述的兔子繁殖序列,就是斐波那契数列。假设斐波那契数列的第n列为F(n),那么可以得到F(n)的递推式:

其中,F(1) = 1,F(2) = 1
斐波那契数列非常著名,其中有一个神奇的特征,随着项数的增大,前项与后项之比越来越接近0.618,被称为黄金分割点,是一个被人类广泛使用的一个奇妙数字。

图6:《蒙娜丽莎》当中的海螺线,处处体现了黄金分割比例
回到文章的开头,在计算汉诺塔问题移动的步数时也得到了一个以自身定义的一个递推式,运用了递归思想来解决问题。递归思想显著帮助了对汉诺塔问题的描述和解答。
四、递归的应用
1. 关于分而治之(Divide and conquer)
分而治之是计算机领域一个重要思想,重复递归手段解决问题。分而治之思想要求,想办法将一个复杂的问题分解为多个子问题,直至这些问题可以被直接解决。所有子问题的计算结果综合起来就是原问题的计算结果。简单来说,分而治之思想就是递归思想的延伸。相当多的算法都有分而治之思想的影子。
比如,排序算法当中著名的归并排序,就是利用了分而治之的策略(小智写过归并排序算法,感兴趣点击传送门)。它将排序结果定义为将两个为原来规模一半的排序结果合并在一起。假设需要排序的规模是n,排序结果定义为F(n),可以定义递推式:

其中,G操作是把两个排序结果合并成一个有序的结果。假如排序所需要的时间为T(n),那么可以定义所需要的计算时间为:
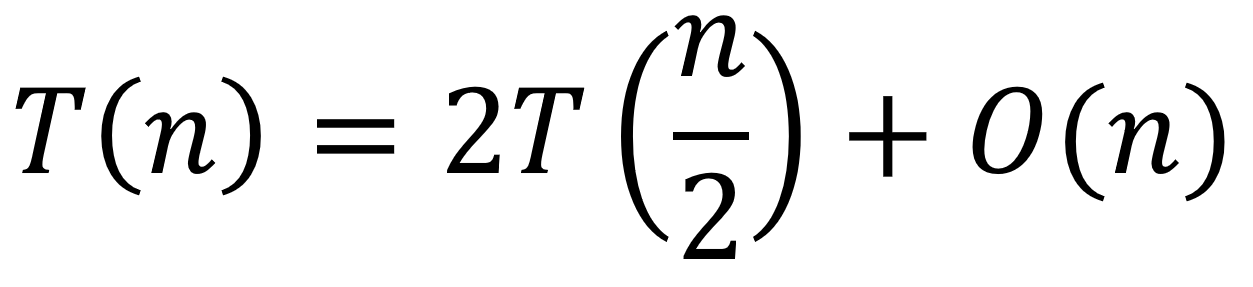
对于一个规模为n的排序问题来说,划分次数是log2 n次,推导可得T(n) = O(n log n),归并排序时间的时间复杂度属于较好的水平了。
2. 关于动态规划(dynamic programming)
动态规划是运筹学的一个分支(小智写过动态规划算法,感兴趣点击传送门)。如果单纯是递归算法,在某些情况下可能会出现非常多的相同子问题,这些子问题对计算效率有很大的影响。
比如,算斐波那契数列F(7),以F(3)为举例,最后要计算F(3)的次数竟然达到5次。随着斐波那契数列的项数增加,若是单纯用递归算法,F(3)计算量必然呈指数级增长。实际上F(3)只需要计算1次就够了,保存起来,需要的时候再调用即可。
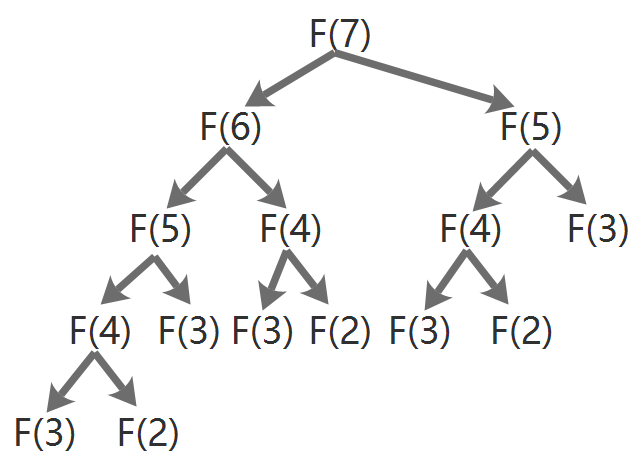
图7:对费波那契数列第7项进行计算涉及到的递归过程
简单来说,动态规划其实就是从这个角度对递归算法进行延伸。动态规划的精妙之处在于,每个子问题只求解一次,并将解保存在一个表格中,当需要再次求解此子问题时,只是简单地通过查表获得该子问题的解,避免大量的重复计算。
3. 关于分形(Fractal)

图8
这条看起来像一朵雪花的曲线,是科赫(Koch)曲线,无限放大后外观上没有变化,这就是一个分形结构。
分形是波兰数学家本华·曼德博(Benoit Mandelbrot)于1975年创造出来的一个词,其原意就是指不规则、破碎等,曼德博想用这个词来描述自然界中传统欧几里德几何学所不能描述的一大类复杂无规的几何对象。
这些几何对象具有自相似的性质,即它们可以分成数个部分,而每一部分都是整体缩小后的形状,就像上图的无限雪花那样。
Koch曲线具备这样的自相似特征,那Koch曲线是怎样画出来的呢?
首先画一个线段,然后把它平分成三段,去掉中间那一段并用两条等长的线段代替。这样,原来的一条线段就变成了四条小的线段。用相同的方法把每一条小的线段的中间三分之一替换为等边三角形的两边,得到了16条更小的线段。然后继续对16条线段进行相同的操作,并无限地进行下去。我们也可以把这个过程写成一个递推式,假设第n次迭代的图形是F(n),那么:

其中G表示将图形的所有线段进行Koch处理,F(1)表示最开始的那条线段。可以看出Koch曲线实际上由自己来定义,是一个简单的递归过程。

图9

图10
诸如Koch曲线、树枝生成等这些分形结构的产生可以运用某个特定规则,不断进行递归,最终可以得到一个完全自相似的结构。

图11:一棵分形树(图片来源:http://robertfathauer.com/FractalTree9.html)
自然界当中存在大量的分形结构,比如树枝、海岸线、山峰、闪电、贝壳、雪花、云朵等等,形成分形的原因非常多。但我觉得有一个非常重要的原因,那就是分形的诞生源自递归,比如树枝的不断地进行同样的生长过程、海岸线不断地受到类似的海浪碰撞、山峰不断地受到类似的风雨侵蚀,这些造就了形状上的分形结构。自然界就是这样的大环境,提供一个不受到干扰的自然演化场景,演化出了这些如此美妙的结构。往大自然更靠近一些,越会发现精彩之处。

图12:分形算法作品《山中晨曦》(图片来源:http://blog.sina.com.cn/s/blog_5fd454d00100i0gu.html)
声明:文章转自【超级数学建模】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











