小明和狮子同被关在一个半径为 10 米的竞技场里,狮子位于竞技场的圆心处,小明则在距离圆心 1 米的地方。两者的最大运动速度都是每秒 1 米。狮子有没有什么必胜策略,使得不管小明怎么跑,它总能在有限的时间里抓住小明?
根据 MathWorld 相关词条的描述,这个问题是由 R. Rado 在 1925 年时提出的。一个经典的“答案”是,狮子只需要始终保持自己与小明在圆盘的同一半径上即可。直觉上看,由于狮子总是处在“内圈”上,因而不管小明跑到了哪里,狮子总能轻松地与小明继续保持在同一半径上;并且,狮子总有足够的余力向小明靠近,严格减小它与小明之间的距离,除非小明是沿着半径方向径直向外跑。由于竞技场的大小是有限的,小明不可能无限地向外跑,因而狮子最终总会追上小明。但是,后来人们发现,这个解法其实是错误的,原因很简单:能不断靠近小明,不一定就能在有限的时间里抓住小明,正如 1/2 + 1/4 + 1/8 + 1/16 + … 永远不会超过 1 一样。最终,A. S. Besicovitch 为小明构造出了一个极其巧妙的策略,使得狮子无论如何都抓不到小明,从而完美地解决了这个问题。不过,MathWorld 的词条里并没有提到这个解法。你能想到这个解法吗?
A. S. Besicovitch 为小明设计的策略如下。游戏开始后,小明首先把接下来的时间分成一小段一小段的,这些时间段的长度依次为\(t_{1},t_{2},t_{3},t_{4},...\)。不妨把竞技场的圆心记作 O ,把小明当前的位置记作 M 。每个时间段开始的时候,小明都会看看此时此刻线段 OM 的位置,并且沿着垂直于 OM 的方向,以最高速度往没有狮子的那一侧跑去(如果狮子的位置恰好位于 OM 所在直线上,则向任意一侧跑去)。容易看出,不管在哪个时间段里,狮子都不可能追到小明。如果把第 i 个时段结束后小明与圆心的距离 OM 记作\(r_{i}\) ,那么由勾股定理可知:
\(r_{i}^{2}=r_{i-1}^{2}+(t_{i}\cdot 1)^{2}=r_{i-1}^{2}+t_{i}^{2}\)
其中\(r_{0}=1\)。
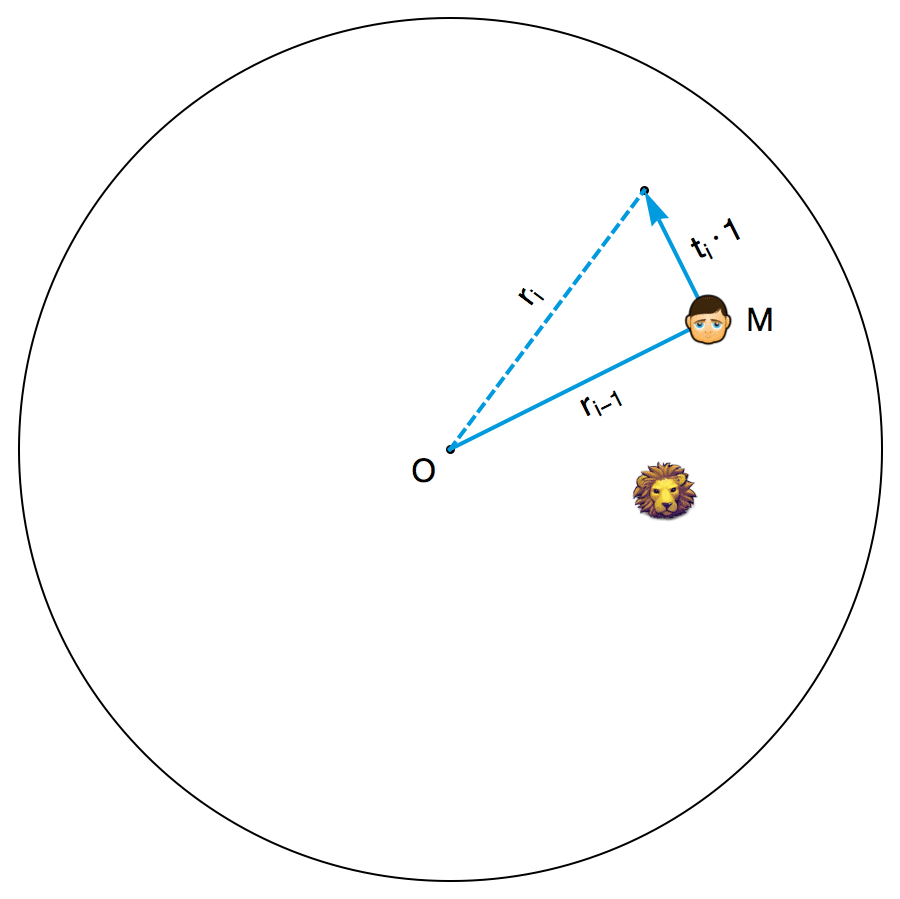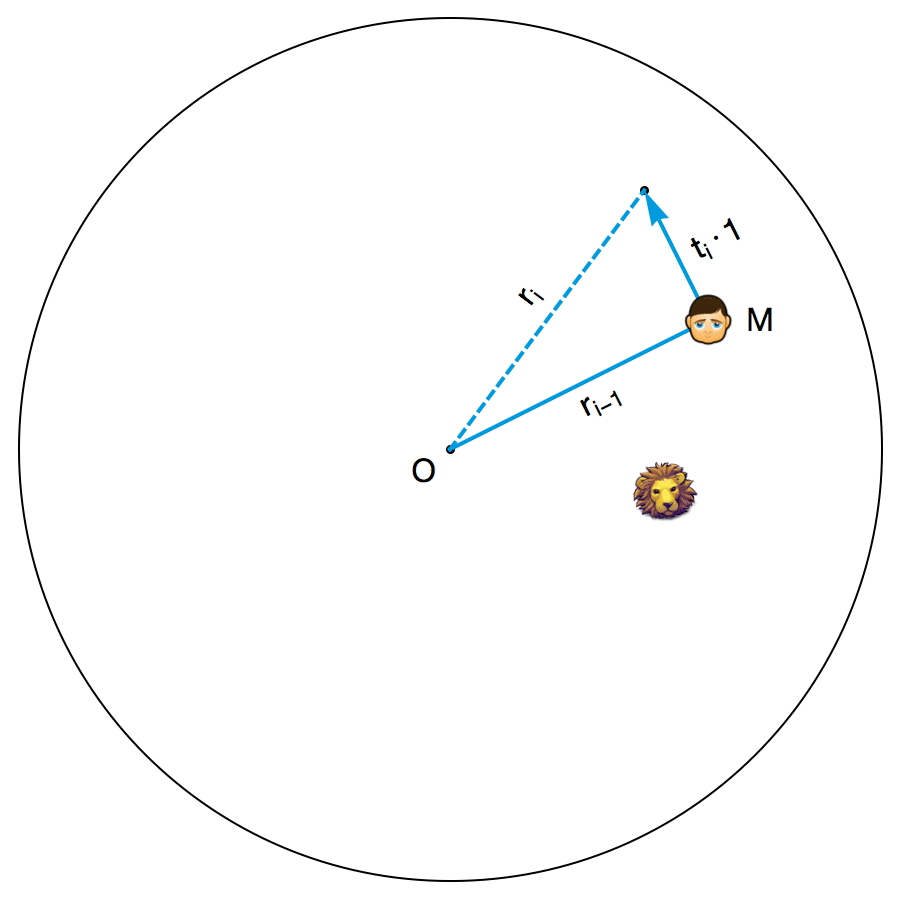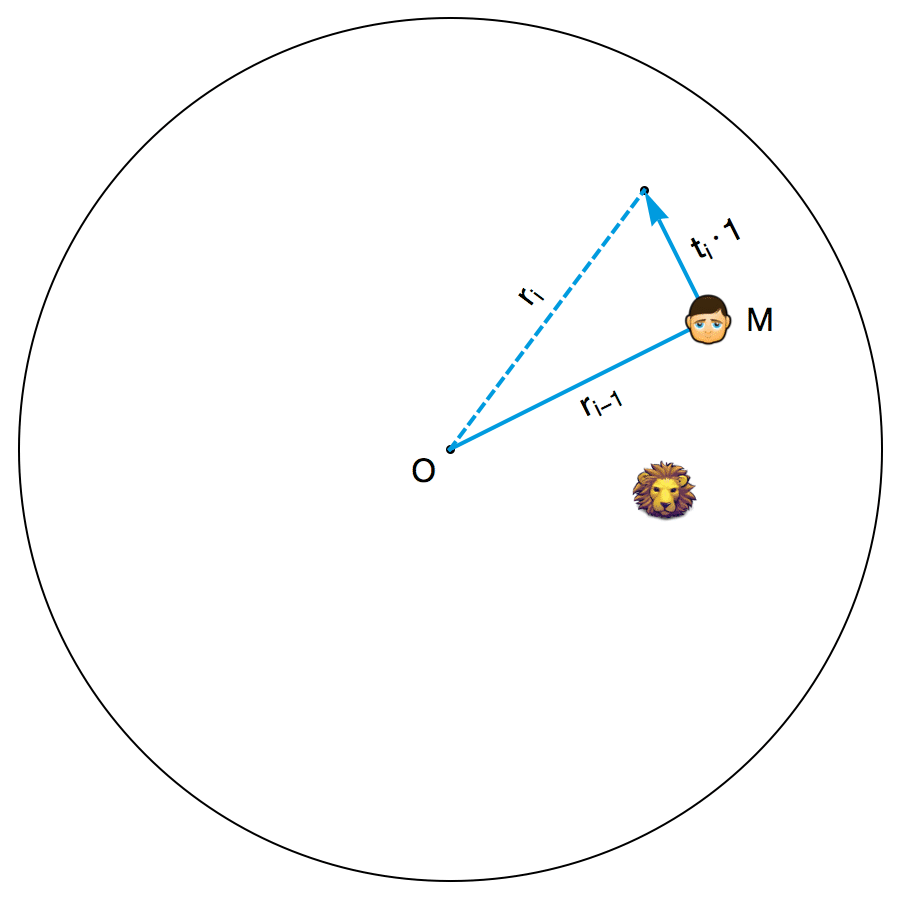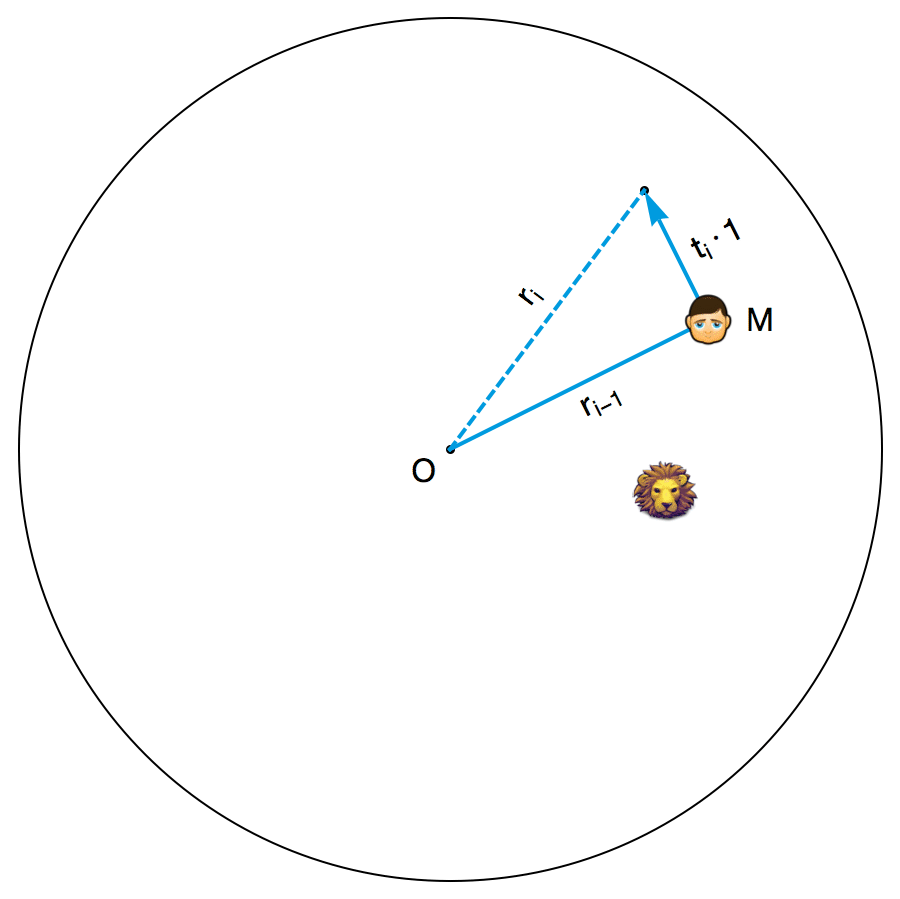
图1
因此,当\(t_{1}+t_{2}+t_{3}+...+t_{n}\)这么多的时间过去以后,小明与圆心的距离 OM 满足
\(OM^{2}=r_{n}^{2}=1^{2}+t_{1}^{2}+t_{2}^{2}+t_{3}^{2}+...+t_{n}^{2}\)
最巧妙的地方来了。令 \(t_{i}=1/i\),那么 \(t_{1}+t_{2}+t_{3}+...\)是发散的,但\(t_{1}^{2}+t_{2}^{2}+t_{3}^{2}+...\)却是收敛的。具体地说:
\(t_{1}+t_{2}+t_{3}+t_{4}+t_{5}+...\)
= 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + 1/9 + …
> 1 + 1/2 + 1/4 + 1/4 + 1/8 + 1/8 + 1/8 + 1/8 + 1/16 + …
= 1 + 1/2 + (1/4) × 2 + (1/8) × 4 + (1/16) × 8 + …
= 1 + 1/2 + 1/2 + 1/2 + 1/2 + …
它显然可以达到任意大。而
\(t_{1}^{2}+t_{2}^{2}+t_{3}^{2}+t_{4}^{2}+t_{5}^{2}...\)
< 1 + 1/(1×2) + 1/(2×3) + 1/(3×4) + 1/(4×5) + …
= 1 + (1 – 1/2) + (1/2 – 1/3) + (1/3 – 1/4) + (1/4 – 1/5) + …
= 1 + 1 – 1/2 + 1/2 – 1/3 + 1/3 – 1/4 + 1/4 – 1/5 + …
≤ 2
因而\(OM^{2}\) 始终不超过 1 + 2 = 3 , OM 的长度也就始终不超过 √3 ≈ 1.732,这远远小于竞技场的半径(事实上, \(OM^{2}\)的极限是\(1+\pi ^{2}/6\) ,可以算出 OM 的极限约为 1.63 )。这说明,不管时间过去了多久,小明始终在坚持运动,并且运动路线始终在可活动范围以内。既然每一个时间段里狮子都无法抓到小明,狮子自然也就永远抓不到小明了。
题目和解答最早应该出自 John Littlewood 的 A Mathematician’s Miscellany 一书当中。图片中的小狮子图标来自这里,小明图标则来自这里。题目里的“策略”一词缺乏形式化的描述,这使得本文的内容非常不严谨,同时还会引发很多其他有趣的讨论,感兴趣的读者可以见这里。
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











