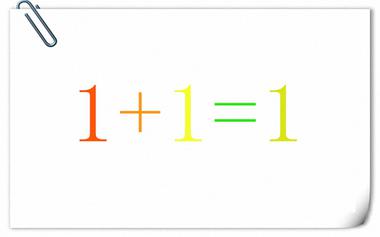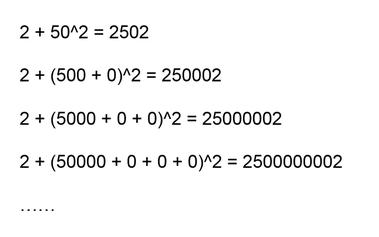神一般的定理，以及神一般的证明
神一般的定理：平面上有三个圆，每一对圆的外公切线交于一点，则三个交点共线。
趣题：连续函数上的水平线段
连续函数f(x)满足f(0)=0且f(1)=0。证明，总能在[0,1]中找到两个数a和b满足b-a=1/2且f(a)=f(b)。换句话说，我们总能画出一条长为1/2的水平线段，它的两个端点都在函数f(x)上。
Sierpinski-Mazurkiewicz悖论：一加一还是等于一
Sierpinski-Mazurkiewicz 悖论是说，存在平面上的一个点集 S ，我们能把它划分成两个子集 A 和 B ，使得 A 旋转 1 弧度后与 S 完全重合， B 平移一个单位后也与 S 完全相同。
八皇后问题算什么，来看看无穷皇后问题吧
八皇后问题有很多变种，不过再怎么也不会比下面这个变种版本更帅：请你设计一种方案，在一个无穷大的棋盘的每一行每一列里都放置一个皇后，使得所有皇后互相之间都不攻击。
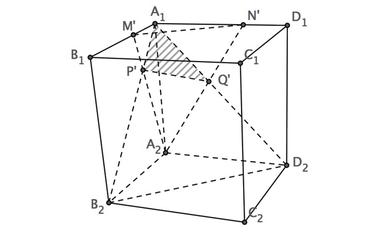
趣题：上哪儿找一个含60度的三角形？
四边形 ABCD 是一个正方形，在 BC 上取一个点 M ，在 CD 上取一个点 N ，使得 BM = CN 。连接 AM 、 AN ，与对角线 BD 分别交于 P 、 Q 两点。求证： BP 、 PQ 、 QD 三条线段一定能组成一个三角
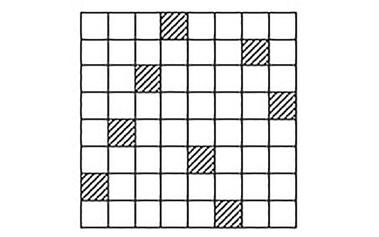
趣题：用奇数个相同的多联骨牌组成轴对称图形
由单位正方形拼接而成的图形叫做多联骨牌。一个有趣的问题是，能否用奇数个相同的多联骨牌拼成一个对称图形？答案是肯定的。
– 1 + 2^7 = 127 这样的算式有多少个？
这样的算式究竟有多少呢？答案是：无穷多。只需要借助本文一开始提到的算式 5^2 = 25 ，我们就能轻易构造出无穷多个同样满足这种神奇性质的算式来。
两两接触的等粗且无限长的圆柱体
大家在吃饭喝酒时是否注意到了这样的事情：三个人碰杯时，每个人的杯子都能同时和其他两个人的杯子相接触，很完美；但是四个人碰杯时，任一时刻总会有两个人碰不到杯，非常尴尬。我们自然引出了这样一个问题：如果n个全等的圆柱体两两相接触，则n最大是多少
数学之美｜双摆曲线方程
本文介绍了双摆曲线方程和双摆图像的Matlab实现，体验双摆曲线之美。
UyHiP趣题：如果每个人都随大流，结果会怎样？
由于 n 个员工一共只能产生 2n 种不同的早饮组合，因此总有一天大家喝的东西会和过去的某一天一模一样，从而产生循环。证明：循环的长度不超过 2 。
零点定理的奇妙应用：平分面积的直线
零点定理是一个大家平时生活中用惯了以至于反而觉得很陌生的一个定理。它的一个比较隐蔽一些的应用便是，对任意一个凸多边形，总存在一条直线把它分成面积相等的两份。
如此排序能成吗？
这种排序法很可能捡了芝麻，丢了西瓜，为了一本书的位置而破坏掉一连串原已排好的书，可谓是鼠目寸光，缺乏远见。我们的问题是，在哪些情况下这样的排序法最终一定能实现排序，哪些情况下可能会陷入永无止境的死循环？