最热门的列表
Benjamin Franklin的另类幻方...
Franklin的16×16幻方，他称它为“史上最神奇的幻方”。在这个幻方中，每一行、每一列和每一个“/”形区域内的数字和都是2056。更不可思议的是，每一个4×4的子正方形内的数字之和也是...
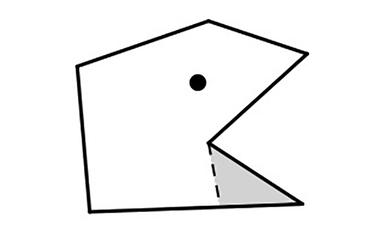
趣题：设计多边形围墙使得对于某一观察点所有的...
在这个六边形的围墙中，如果站在图中圆点的位置，那么有两面墙不能被完全看见（其中一面墙完全看不见）。能否设计出一个多边形围墙，使得站在围墙里面的某个地方后，所有的墙都至少有一部分是不可见的？
奇妙的心电图数列
心电图数列有一个很漂亮的数学事实：所有的自然数都出现在了这个数列中。由这个数列的定义，每个数最多也只能出现一次。因此，心电图数列是全体自然数的一个排列。这个结论的证明堪称经典。
除了正多面体，骰子还可以做成哪些形状？
事实上，对于骰子来说， 正多面体不是必要的。至少不需要那么“正”——只需要满足多面体每个面的地位都相同就可以了。例如，取两个全等的正 n 棱锥，底面和底面互相粘在一起，就能得到一个有 2n ...
1 4 6 4 1不是唯一答案，我们还有Ra...
Rascal 三角形的神奇之处：尽管每个数都是由两数相除得来的，但它们保证都是整数！你能看出这是为什么吗？
视频 |【PBS无尽数学】利用图着色求解金刚...
图着色问题可能看起来很简单，但背后却异常的复杂。本次视频中Kelsey讨论了Sudoku，四色定理，Hadwiger Nelson问题以及如何使用图着色来安排调度超级英雄们来拯救地球的最有效...
趣题：用奇数个相同的多联骨牌组成轴对称图形
由单位正方形拼接而成的图形叫做多联骨牌。一个有趣的问题是，能否用奇数个相同的多联骨牌拼成一个对称图形？答案是肯定的。
数学是猫咪的语言！随意一个pose都是艺术
数学是猫的语言，这一组斐波那契数列不同于来自印度数学家Pingala，或意大利数学家Leonardo Fibonacci所研究的。这是喵星人的斐波那契数列！
为什么这十个公式是世界上最美的
本文为大家细数那些年见过的最美数学公式。
数学之美：无处不在的函数
Nikki Graziano是一个数学家，同时也是个摄影师。她的爱好是把两者结合起来，形成一种独特的数学艺术。这个名叫“发现函数”的系列里，她就展示了在自然界里的数学原理
数学之美｜细数那些历史上的数学诗
我国堪称“诗的王国”，真的一点不假，打开历史长卷，我国的诗歌品类繁多，浩如烟海，“数学诗”乃沧海一粟，却别具一格，或写景、或抒怀、或记事、或计算，数学与诗歌浑然一体，读来真是一种享受。
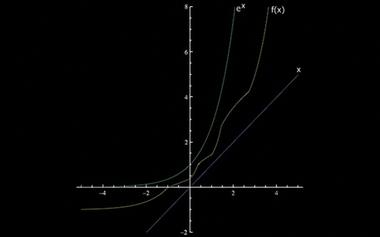
原来函数也是有平方根的
e^x的“平方根”究竟是什么样的呢？不妨假设满足要求的f(x)也是一个连续递增的函数，那么它的增长速度必然超过一切多项式函数（否则迭代的结果还是多项式），同时也必然小于一切指数形式的函数。
