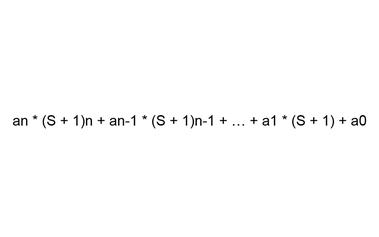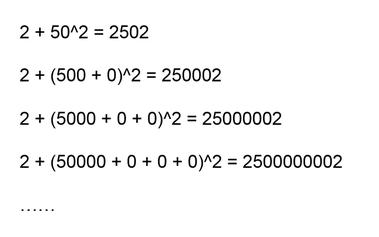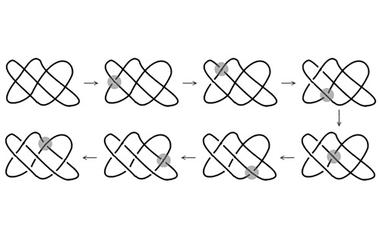- 首页
- 资讯▪报告
- 数据中心
涨停股票池
15:50 PM -- Jun 16,2023换手率榜
15:50 PM -- Jun 16,202310%涨跌幅榜
15:50 PM -- Jun 16,202320%涨跌幅榜
15:50 PM -- Jun 16,202360天涨跌幅榜
15:50 PM -- Jun 16,2023年初至今涨跌幅榜
15:50 PM -- Jun 16,2023主力流入榜
15:50 PM -- Jun 16,2023量比榜
15:50 PM -- Jun 16,2023总市值榜
15:50 PM -- Jun 16,2023流通市值榜
15:50 PM -- Jun 16,2023市净率榜
15:50 PM -- Jun 16,2023市盈率榜
15:50 PM -- Jun 16,2023概念换手率榜
15:50 PM -- Jun 16,2023概念涨跌幅榜
15:50 PM -- Jun 16,2023概念60天涨跌幅榜
15:50 PM -- Jun 16,2023概念年初至今涨跌幅榜
15:50 PM -- Jun 16,2023概念主力流入榜
15:50 PM -- Jun 16,2023行业换手率榜
15:50 PM -- Jun 16,2023行业涨跌幅榜
15:50 PM -- Jun 16,2023行业60天涨跌幅榜
15:50 PM -- Jun 16,2023行业年初至今涨跌幅榜
15:50 PM -- Jun 16,2023行业主力流入榜
15:50 PM -- Jun 16,2023 - 关于我们
最新的列表
趣题:两步猜出多项式的各项系数
有一个黑匣子,黑匣子里有一个关于 x 的多项式 p(x) 。我们不知道它有多少项,但已知所有的系数都是正整数。每一次,你可以给黑匣子输入一个整数,黑匣子将返回把这个整数代入多项式后的值。有一...
除了正多面体,骰子还可以做成哪些形状?
事实上,对于骰子来说, 正多面体不是必要的。至少不需要那么“正”——只需要满足多面体每个面的地位都相同就可以了。例如,取两个全等的正 n 棱锥,底面和底面互相粘在一起,就能得到一个有 2n ...
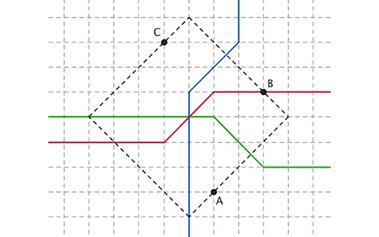
出租车几何学:一个全新的几何世界
在理想模型中,假设每条道路都是水平或者竖直的,那么只要你朝着目标走(不故意绕远路),不管你怎样走,花费的路程都是一样的。今天,我看到了一个非常有意思的名词——出租车几何学,其名称就来源于这样...
100个囚犯和灯泡的那些事儿(上)
说有 100 个囚犯分别关在 100 间牢房里。牢房外有一个空荡荡的房间,房间里有一个由开关控制的灯泡。初始时,灯是关着的。看守每次随便选择一名囚犯进入房间,但保证每个囚犯都会被选中无穷多次...
– 1 + 2^7 = 127 这样的算式有...
这样的算式究竟有多少呢?答案是:无穷多。只需要借助本文一开始提到的算式 5^2 = 25 ,我们就能轻易构造出无穷多个同样满足这种神奇性质的算式来。
最热门
-
莫比乌斯圈和克莱因瓶的美学...
March 08, 2018 -
扭曲的艺术——“怪圈”莫比...
March 07, 2018 -
数学之美|双摆曲线方程
November 10, 2017 -
【全微分】- 图解高等数学...
January 19, 2018 -
【二次曲面】- 图解高等数...
January 19, 2018 -
【多元函数极值/拉格朗日乘...
January 19, 2018
最多人收藏
-
11:12 AM - March 09, 2018
我眼中的数学之美(更正版)
-
06:22 AM - November 02, 2017
最具争议的12个数学事实,测试和提升...
-
05:19 PM - May 11, 2018
指数函数和自然对数
-
08:42 AM - November 01, 2017
为什么这十个公式是世界上最美的
-
03:38 PM - February 26, 2018
非传递性骰子:A比B好,B比C好,A...
-
02:22 PM - February 01, 2018
如何理解置信区间?