最近20年的癌症研究开发了日新月异的癌症治疗剂,领域包括化学治疗、靶向治疗、免疫治疗等。然而鉴于癌症病人数量有限且分布稀疏,所以仅凭临床试验很难找到最优化的治疗方案。从可行性出发,我们需要首先预测各种治疗方案的的效果,然后挑选预期较好的方案进入临床检验。
The recent 20 years of cancer research has witnessed rapidly growing varieties of treatment agents for cancer, in the areas of cytotoxic/cytostatic chemotherapy, targeted therapy, immunotherapy and other therapies. However, the identification of optimal treatment strategies through clinical trials is hampered by the contradiction between the limited/sparsely distributed patients and the near-infinite combination treatment strategies. Practically, it is important to prospectively predict the outcomes for each treatment strategy, and then assess the favorable options in the clinic.
由于癌症发生发展过程中的随机性、非线性、和异质性,我们无法仅凭推理来预判治疗方案的效果。而数学建模在模拟癌症动态发展和预测治疗效果中显示出了强大的潜质。例如,Tang和同事根据慢性粒细胞白血病人用药过程中癌细胞数量的动态变化,预测药物格列卫可以攻击并减少白血病干细胞[1];Chmielecki和同事模拟非小细胞肺癌对药物厄洛替尼抗性的动态过程,以此优化用药时间安排并延长了厄洛替尼对癌症的有效时间[2];Haeno和同事研究胰腺癌转移和发展的速率,并预测尽早使用抑制胰腺癌细胞生长的药物治疗效果会好于前期手术切除[3];Leder和同事通过对胶质母细胞瘤对放疗反应的动力学研究,预测了优化的放疗剂量和时间安排,并在动物模型中得到了验证[4]。
Because of the stochasticity, non-linearity, and heterogeneity involved in the development of cancer, the outcomes of different treatments cannot be prospectively determined by verbal reasoning alone. Consequently, mathematical modeling has shown tremendous potential in characterization of cancer development and prediction of treatment outcomes. For example, Tang et al. studied the dynamics of leukemic load in chronic myeloid leukemia (CML) patients treated with Gleevec, and predicted that Gleevec has the potential to target CML-stem cells [1]; Chmielecki et al. modeled the evolution of erlotinib resistance in non-small cell lung cancer (NSCLC), and predicted alternative treatment strategies that could prolong the benefit of erlotinib [2]; Haeno et al. simulated metastasis of pancreatic cancer (PC), and predicted that therapies that reduce the growth rate of PC cells are superior to upfront tumor resection [3]; Leder et al. characterized dynamics of glioblastoma (GBM) in response to radiotherapy, and managed to predict superior dosing schedules for radiotherapy and improved GBM survival in animal model [4].
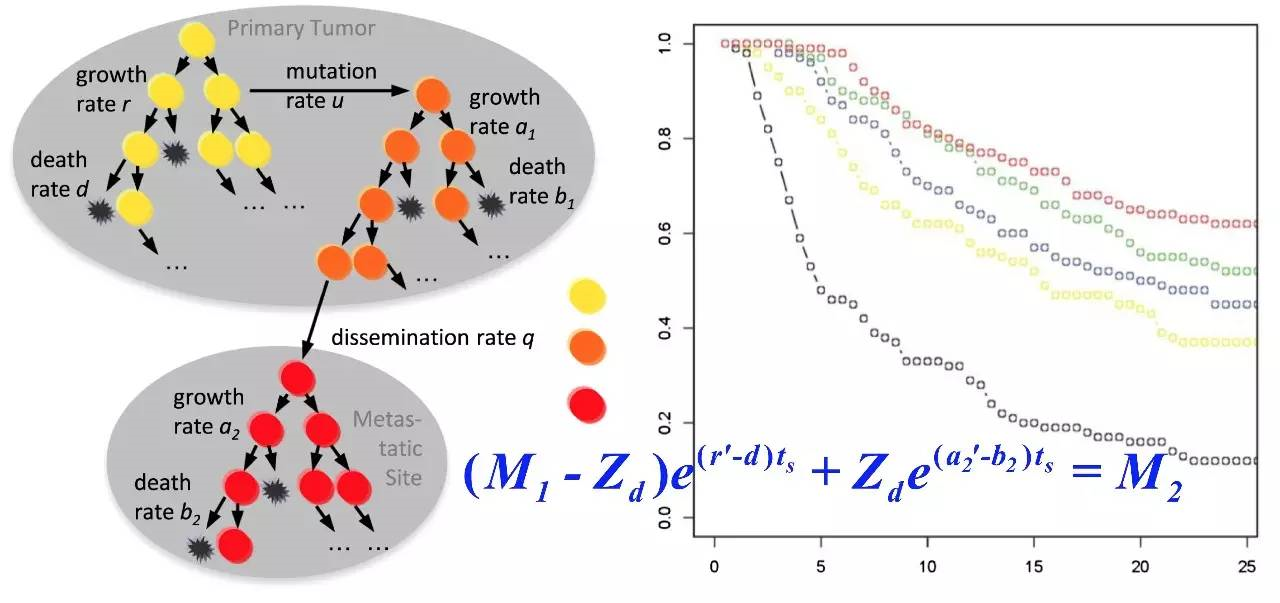
图1
今年,一项来自多伦多大学Benjamin Neel实验室的研究针对高等级浆液性卵巢癌(HG-SOC)进行了动态研究,并模拟了一系列优化的治疗/筛查方案[5]。根据近300个病人的临床数据,我们首先建立了一个随机分支模型模拟化疗抗性的演变过程。根据估量得到的癌细胞转变率,我们推测绝大多数HG-SOC病人在诊断之初体内已经有大于103个抗化疗癌细胞。我们比较了不同治疗方案,并预测前期手术切除加辅助化疗效果好于前期化疗辅以肿瘤细胞减灭术,因为前者会更有效地去除抗化疗癌细胞。此外,我们检验了提早诊断对HG-SOC患者生存的影响。针对复发癌症的提早诊断,我们预测无论利用CA125或更灵敏的检验方法,都不会延长患者的生存时间,因为对复发HG-SOC的提早治疗无法有效去除抗化疗细胞。相反,针对未接受过治疗的患者,我们预测提早诊断治疗将会延长生存预期并提高治愈率。
A recent study from Dr. Benjamin Neel’s lab at University of Toronto studied the clinical dynamics of high-grade serous ovarian cancer (HG-SOC), and investigated the optimal management strategies for this disease [5]. We built a stochastic branching model to simulate the evolution of chemotherapy resistance, based on clinical data from nearly 300 HG-SOC patients. After estimating the conversion rate from chemo-sensitive to chemo-resistant cells, we determined that most HG-SOC patients likely harbor >103 chemo-resistant cells at diagnosis. We then compared different temporal orders of treatment, and predicted that upfront optimal surgery followed by chemotherapy should be superior to upfront chemotherapy with interval surgery, largely because it more efficiently depletes chemo-resistant cells. Furthermore, we interrogated the benefits of early diagnosis of HG-SOC. We recapitulated the clinical finding that CA125-based earlier diagnosis of relapsed cancer does not improve overall survival, and further predicted that more sensitive detection methods are also unlikely beneficial with current standard chemotherapy, because it does not help deplete the chemo-resistant cells. By contrast, our model predicts that for treatment-naïve cancer, early detection could improve survival time and increase chances of cure.
随着高通量测序技术和精准医疗的发展,我们更加需要模拟癌症进化发展的定量模型来促进多疗法联合治疗以及有预见地处理癌症复发。对于未来数学模型在癌症领域的应用,我认为将会有以下几个趋势:(1)将基因组数据融入数学模型用于模拟和预测癌症克隆演变动态,向及时精准医疗的目标迈进;(2)结合机器学习技术和数学模型,根据临床和实验数据推断治疗抗性模式,有助于发现在癌症不同发展时期克服抗性的新靶标;(3)利用数学模型预测免疫治疗的有效性并探索免疫治疗和传统治疗的结合疗法,促进多种疗法协同去除癌症。
With the advent of high-throughput sequencing and precision medical care for cancer, there is increasing feasibility and demand for quantitative models of cancer evolution dynamics, in order to facilitate effective combination therapy and/or prospectively prepare for disease recurrence. For future application of mathematical modeling in cancer prevention/treatment, I speculate several trends will form and exhibit significant impacts in the field: (1) incorporation of genomic data and mathematical modeling to monitor and predict dynamic clonal evolution of cancer, which would help achieve punctual precision medical care; (2) application of mathematical modeling and machine learning techniques on clinical/experimental data to extrapolate treatment resistance patterns, which would help identify additional targets for different stages of cancer development; (3) application of mathematical modeling in immunotherapy to predict the likelihood of response and explore the combination of immunotherapy and conventional therapies, which would facilitate synergistic depletion of cancer using different therapies.
参考文献(References):
[1] Tang, M. et al. Dynamics of chronic myeloid leukemia response to long-term targeted therapy reveal treatment effects on leukemic stem cells. Blood 118, 1622–1631 (2011).
[2] Chmielecki, J. et al. Optimization of dosing for EGFR-mutant non-small cell lung cancer with evolutionary cancer modeling. Sci. Transl. Med. 3, 90ra59 (2011).
[3] Haeno, H. et al. Computational modeling of pancreatic cancer reveals kinetics of metastasis suggesting optimum treatment strategies. Cell 148, 362–75 (2012).
[4] Leder, K. et al. Mathematical modeling of pdgf-driven glioblastoma reveals optimized radiation dosing schedules. Cell 156, 603–616 (2014).
[5] Computational modeling of serous ovarian carcinoma dynamics: Implications for screening and therapy. at http://www.abstractsonline.com/Plan/ViewAbstract.aspx?mID=3682&sKey=0b3c3568-eecc-4a05-b2a6-eca0a1f1b029&cKey=5b08121c-eeee-4ef7-be71-c321f3ebfd4f&mKey=19573a54-ae8f-4e00-9c23-bd6d62268424.
作者简介(Author ' s Biography):

图2:顾圣青
顾圣青顾圣青毕业于北京大学元培计划学院,于2008-2015年在多伦多大学医学生物物理系师从Benjamin Neel教授进行癌症信号转导和癌症数学模型的跨学科研究。现在研究兴趣包括通过数学模型模拟癌症进化动力学以及通过机器学习研究癌症抗药机理。
邮箱地址:Sgu@uhnres.utoronto.ca
Shengqing Gu obtained his B.S. degree from Yuanpei program in Peking University. In 2008, he joined the lab of Dr. Benjamin Neel in Department of Medical Biophysics at University of Toronto to participate in interdisciplinary research involving signaling pathways in cancer and mathematical modeling of cancer. His current research interests include mathematical modeling of cancer evolution dynamics and machine learning of therapy resistance mechanisms.
Email: Sgu@uhnres.utoronto.ca
稿件来源 (Sources of the Article):
本文由加拿大多伦多大学顾圣青同学投稿,海外华人医疗创新者协会团队编辑和推送!
若感兴趣分享您在医疗领域的专业视角和看法,欢迎投稿,回复投稿 或 tougao获取相关信息或直接发邮件至article_submission@ochis.org。
This article was submitted by Shengqing Gu from University of Toronto. It was edited and published by Overseas Chinese Healthcare Innovator Society (OCHIS).
If you are interested in sharing your professional perspective on healthcare associated topics, welcome to summit an article to us. In terms of article submission, please reply directly through the WeChat public platform with the key word tougao for the details or you could just email article_submission@ochis.org.
版权声明 (Copyright):
本文所有内容版权归海外华人医疗创新者协会(OCHIS)所有,未经授权,不得转载、摘编或利用其他方式使用上述内容。违反上述声明者,OCHIS将在天津市滨海新区健康促进研究会协助下追究其相关法律责任。
Copyright © Overseas Chinese Healthcare Innovator Society (OCHIS). All rights reserved. No part of this article may be reproduced, copied, modified or transmitted in any form, without the prior written consent of OCHIS. Sharing without authorization is an infringement of local copyright law.











