最热门的列表
Pick定理的几个出人意料的应用
Pick定理是说，在一个平面直角坐标系内，如果一个多边形的顶点全都在格点上，那么这个图形的面积恰好就等于边界上经过的格点数的一半加上内部所含格点数再减一。
Runge现象：多项式插值不见得次数越高越准...
1901年，Carl David Tolmé Runge意外地发现，用插值多项式逼近函数f(x)=1/(1+25x^2)时出现了一些反常的现象。
非常奇妙的证明：图形必在格点之外
问题：设想一个平面上布满间距为1的横纵直线，形成由一个个1×1正方形组成的网格。任意给一个面积小于1个单位的图形，证明这个图形总能放在网格中而不包含任何一个格点。
趣题：用树来表示数
每棵树代表一个质数，一个森林（若干个树放一块儿）就表示这些质数的乘积；如果一个森林表示的是n，在这个森林下方添加一个公共根，就构成了新的质数——第n个质数。这个东西牛就牛在，它建立了一个自然...
手游出海周报 | 2020全球游戏收入126...
手游出海一周要闻汇总2021.01.04-01.10
趣题：每一列中至少有一个数字0或数字9
任意写下一个数，再在它下面写下它的2倍、3倍、4倍、……、9倍。把这些数按位对齐，每一列里恰好有9个数字（前面几行中的首位为空时该位置视作0）。证明，每一列中至少有一个数字0或者数字9。
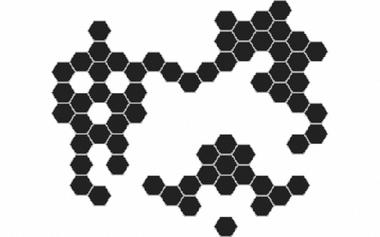
能平铺平面，却不能周期性地平铺平面
虽然正方形、长方形、正六边形等图形都能平铺整个平面，但平铺的方式却非常无聊，不过是同一种模式不断重复罢了。有没有什么“非平凡”的平铺方案呢？本文就给大家看这样一个图形。
手游出海周报 | 2020年推特最火的十大游...
手游出海一周要闻汇总2021.01.11-01.17
19有什么特别的地方？
把从 1/19 到 18/19 的所有分数展开成小数，得到一个 18 × 18 的数字方阵。这个数字方阵有什么特别的地方呢？
最帅的Menelaus定理证明方法
Menelaus 定理的证明方法有很多，今天我见到了我所见过的证明方法中最帅的一种，它解决了之前很多证明方法缺乏对称性的问题，完美展示了几何命题中的对称之美。
集数学与艺术于一体的几何幻方
Lee Sallows做了一个网站，收集了很多在几何意义上也成立的幻方，集数学与艺术于一体，为传统意义的幻方赋予了新的生命，大家来欣赏一下吧。
这个图形有什么牛B的地方？
对一个正六边形的6个相邻六边形进行黑白二染色，一共可以得到64种构造。
