最热门的列表
数学之美：无处不在的函数
Nikki Graziano是一个数学家，同时也是个摄影师。她的爱好是把两者结合起来，形成一种独特的数学艺术。这个名叫“发现函数”的系列里，她就展示了在自然界里的数学原理
选举制度的学问
每个投票者把自己手中的票投给其中一位候选人，得票数最多的候选人即获胜，因为他的支持者最多。这看上去似乎挺合理。但在实际生活中，这种选举制度并不见得总是合理的，得票数最多的候选人很可能并不是大...
玩转内接多边形（二）：任意多边形内均存在内接...
是否任意一个多边形内都能找到内接矩形呢？答案也是肯定的。本文对它的证明真可谓是巧妙到了诡异的地步，真不知是谁想出来的。
看视频，领悟数学之美 2
用欣赏的眼光看数学，就会看到她青春靓丽的一面，她的惊艳之美！
关于123456789：一个难以解释的数学巧...
将123456789翻一倍，你会发现结果仍然是这9个数字的一个排列：123456789 x 2 = 246913578。我们再次将246913578翻倍，发现：246913578 x 2 =...
虐童概率论：没有哪个孩子是一座孤岛
在概率论中概率接近0的事件，它在一次实验中是几乎不可能会发生的，但随着试验重复次数的无限增多，小概率事件必然发生。
魅力无穷的完全数
公元前3世纪时，古希腊数学家对数字情有独钟。他们在对数的因数分解中，发现了一些奇妙的性质，如有的数的真因数之和彼此相等，于是诞生了亲和数；而有的真因数之和居然等于自身，于是发现了完全数。6是...
神奇的分形艺术（四）：Julia集和Mand...
考虑复数函数f(z)=z^2+c，不同的复数c对应着不同的Julia集。也就是说，每取一个不同的c你都能得到一个不同的Julia集分形图形，并且令人吃惊的是每一个分形图形都是那么美丽。Man...
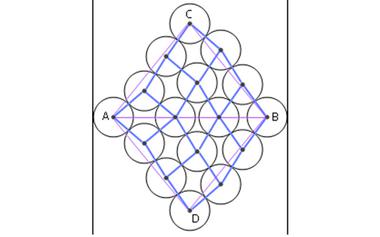
趣题：货架上的听装可乐
有个放听装可乐的货架，它的宽度要比四听可乐的直径稍微大一些。把10听可乐放进这个货架里，堆叠成一个三角形。虽然底下三层可乐罐歪歪斜斜有高有低，但最顶上的那听可乐一定位于货架的正中心，也就是说...
藏在身体的数学
一个鲜为人知的事实是我们的身体也试图教我们高等的数学，只要我们希望如此。来看婴儿的第一个发式，头发中间那个可爱的漩涡，按数学的说法，就是一个“奇点”，这个婴儿的头发似乎无法决定该往哪个方向生...
视频 | 国际象棋的“骑士”与马尔科夫链
国际象棋中如果一个骑士（马）经过随机移动，最后又返回到初始的位置。可能两步就能返回，也可能骑士需要很长时间才找到“回家”的路，那么问题是究竟要平均要跳多少次呢？
2019年度中国影视内容消费者年度研究报告
本报告由“电影消费者属性与观影行为”、“院线电影产品的消费者认知与评价”和“剧集消费者属性与观剧行为”三部分组成，为中国影视产业描摹出更加生动和清晰的消费者画像。
