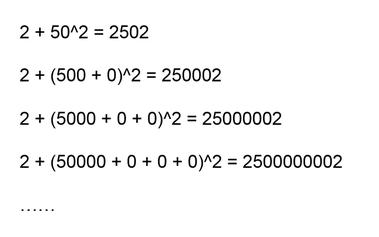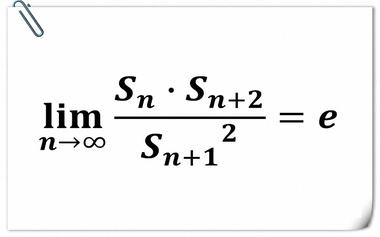- 首页
- 资讯▪报告
- 数据中心
涨停股票池
15:50 PM -- Jun 16,2023换手率榜
15:50 PM -- Jun 16,202310%涨跌幅榜
15:50 PM -- Jun 16,202320%涨跌幅榜
15:50 PM -- Jun 16,202360天涨跌幅榜
15:50 PM -- Jun 16,2023年初至今涨跌幅榜
15:50 PM -- Jun 16,2023主力流入榜
15:50 PM -- Jun 16,2023量比榜
15:50 PM -- Jun 16,2023总市值榜
15:50 PM -- Jun 16,2023流通市值榜
15:50 PM -- Jun 16,2023市净率榜
15:50 PM -- Jun 16,2023市盈率榜
15:50 PM -- Jun 16,2023概念换手率榜
15:50 PM -- Jun 16,2023概念涨跌幅榜
15:50 PM -- Jun 16,2023概念60天涨跌幅榜
15:50 PM -- Jun 16,2023概念年初至今涨跌幅榜
15:50 PM -- Jun 16,2023概念主力流入榜
15:50 PM -- Jun 16,2023行业换手率榜
15:50 PM -- Jun 16,2023行业涨跌幅榜
15:50 PM -- Jun 16,2023行业60天涨跌幅榜
15:50 PM -- Jun 16,2023行业年初至今涨跌幅榜
15:50 PM -- Jun 16,2023行业主力流入榜
15:50 PM -- Jun 16,2023 - 关于我们
最热门的列表
– 1 + 2^7 = 127 这样的算式有...
这样的算式究竟有多少呢?答案是:无穷多。只需要借助本文一开始提到的算式 5^2 = 25 ,我们就能轻易构造出无穷多个同样满足这种神奇性质的算式来。
让你看到函数图象在无穷远处的样子
当x从-π/2连续地增加到π/2时,x的正切值将会从负无穷连续地增加到正无穷。因此,为了展示出y=f(x)在无穷远处的样子,我们可以画出tan(y)=f(tan(x))在(-π/2,π/2)...
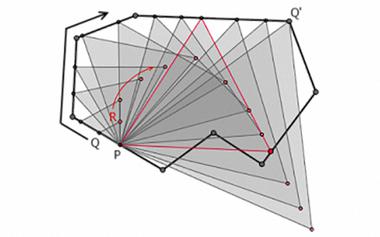
Cramer悖论:线性代数的萌芽
虽说数学悖论大多是些让人越想越糊涂的逻辑思维游戏,但也有不少悖论来自实实在在的数学问题。那些最难解决的悖论甚至为数学新分支的开创带来了足够的动机,Cramer悖论就是一个漂亮的例子。
杨辉三角中的自然底数 e
2012年,Harlan Brothers发现了杨辉三角中的一个有趣的事实。不妨把杨辉三角第n行的所有数之积记作sn,那么随着n的增加,sn·sn+2/sn+12会越来越接近e≈2.718。...
最新的
-
解决一个预测类数学建模问题...
November 26, 2020 -
视频 | 用3D动画可视化...
May 14, 2018 -
比特币背后的数学
May 14, 2018 -
从群论角度理解欧拉公式
May 14, 2018 -
指数函数和自然对数
May 11, 2018 -
视频 | 复数及复变函数的...
May 11, 2018
最多人收藏
-
11:12 AM - March 09, 2018
我眼中的数学之美(更正版)
-
06:22 AM - November 02, 2017
最具争议的12个数学事实,测试和提升...
-
10:47 AM - February 05, 2018
选举制度的学问
-
10:59 AM - January 22, 2018
【用几何来求导】- 微积分的本质 0...
-
09:07 AM - March 08, 2018
拓扑为何?
-
03:26 AM - October 27, 2017
古今建筑中的数学思想