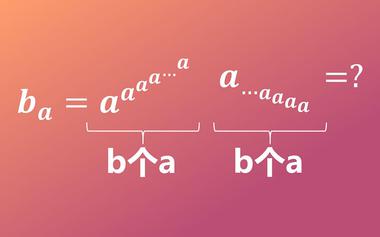- 首页
- 资讯▪报告
- 数据中心
涨停股票池
15:50 PM -- Jun 16,2023换手率榜
15:50 PM -- Jun 16,202310%涨跌幅榜
15:50 PM -- Jun 16,202320%涨跌幅榜
15:50 PM -- Jun 16,202360天涨跌幅榜
15:50 PM -- Jun 16,2023年初至今涨跌幅榜
15:50 PM -- Jun 16,2023主力流入榜
15:50 PM -- Jun 16,2023量比榜
15:50 PM -- Jun 16,2023总市值榜
15:50 PM -- Jun 16,2023流通市值榜
15:50 PM -- Jun 16,2023市净率榜
15:50 PM -- Jun 16,2023市盈率榜
15:50 PM -- Jun 16,2023概念换手率榜
15:50 PM -- Jun 16,2023概念涨跌幅榜
15:50 PM -- Jun 16,2023概念60天涨跌幅榜
15:50 PM -- Jun 16,2023概念年初至今涨跌幅榜
15:50 PM -- Jun 16,2023概念主力流入榜
15:50 PM -- Jun 16,2023行业换手率榜
15:50 PM -- Jun 16,2023行业涨跌幅榜
15:50 PM -- Jun 16,2023行业60天涨跌幅榜
15:50 PM -- Jun 16,2023行业年初至今涨跌幅榜
15:50 PM -- Jun 16,2023行业主力流入榜
15:50 PM -- Jun 16,2023 - 关于我们
最喜爱的列表
为何美洲蝉中意17这个质数?
在北美洲的森林里栖息着一种生命周期十分古怪的蝉类。这些蝉藏于地下长达17年,其间甚少活动,而在第17个年头的五月份,这些蝉只会集体钻出地面侵入森林,而侵入每英亩森林的蝉只数量就多达百万。
又一个比较诡异的悖论
假如我们拿到了100元钱的信封,那么换一个信封得到1000元的概率是得到10元的概率的一半。也就是说,如果我们拿到了x元钱,换一个信封的话有1/3的概率多得9x元,有2/3的概率失去0.9x...
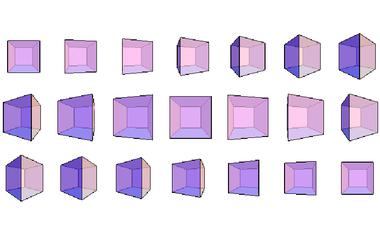
除了正多面体,骰子还可以做成哪些形状?
事实上,对于骰子来说, 正多面体不是必要的。至少不需要那么“正”——只需要满足多面体每个面的地位都相同就可以了。例如,取两个全等的正 n 棱锥,底面和底面互相粘在一起,就能得到一个有 2n ...
比乘法更大的是乘方,比乘方更大的是什么?
乘方之上究竟是什么?下面,有请我们的主角——超级幂登场!超级幂是一个极为厉害的运算,它的增长速度非常惊人,在很小的数之间进行超级幂运算,就有可能得到一个巨大的天文数字。
最新的
-
解决一个预测类数学建模问题...
November 26, 2020 -
视频 | 用3D动画可视化...
May 14, 2018 -
比特币背后的数学
May 14, 2018 -
从群论角度理解欧拉公式
May 14, 2018 -
指数函数和自然对数
May 11, 2018 -
视频 | 复数及复变函数的...
May 11, 2018
最多人收藏
-
11:12 AM - March 09, 2018
我眼中的数学之美(更正版)
-
06:22 AM - November 02, 2017
最具争议的12个数学事实,测试和提升...
-
10:46 AM - February 28, 2018
趣题:设计多边形围墙使得对于某一观察...
-
02:21 PM - February 05, 2018
让你看到函数图象在无穷远处的样子
-
11:19 AM - January 22, 2018
【指数函数求导】- 微积分的本质 0...
-
10:42 AM - March 08, 2018
星座和数学家,看看你的星座适合学数学...