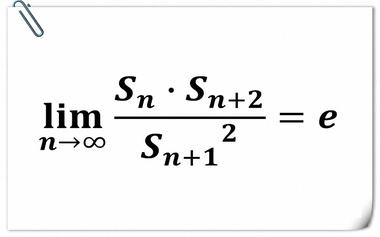- 首页
- 资讯▪报告
- 数据中心
涨停股票池
15:50 PM -- Jun 16,2023换手率榜
15:50 PM -- Jun 16,202310%涨跌幅榜
15:50 PM -- Jun 16,202320%涨跌幅榜
15:50 PM -- Jun 16,202360天涨跌幅榜
15:50 PM -- Jun 16,2023年初至今涨跌幅榜
15:50 PM -- Jun 16,2023主力流入榜
15:50 PM -- Jun 16,2023量比榜
15:50 PM -- Jun 16,2023总市值榜
15:50 PM -- Jun 16,2023流通市值榜
15:50 PM -- Jun 16,2023市净率榜
15:50 PM -- Jun 16,2023市盈率榜
15:50 PM -- Jun 16,2023概念换手率榜
15:50 PM -- Jun 16,2023概念涨跌幅榜
15:50 PM -- Jun 16,2023概念60天涨跌幅榜
15:50 PM -- Jun 16,2023概念年初至今涨跌幅榜
15:50 PM -- Jun 16,2023概念主力流入榜
15:50 PM -- Jun 16,2023行业换手率榜
15:50 PM -- Jun 16,2023行业涨跌幅榜
15:50 PM -- Jun 16,2023行业60天涨跌幅榜
15:50 PM -- Jun 16,2023行业年初至今涨跌幅榜
15:50 PM -- Jun 16,2023行业主力流入榜
15:50 PM -- Jun 16,2023 - 关于我们
最新的列表
五个有趣的拓扑变换问题
如果你喜欢上次的空间想象能力挑战,你一定会喜欢V.V.Prasolov的Intuitive Topology一书。书中的第一章有五个非常经典的“拓扑变换”类谜题,在此与大家分享。
两两接触的等粗且无限长的圆柱体
大家在吃饭喝酒时是否注意到了这样的事情:三个人碰杯时,每个人的杯子都能同时和其他两个人的杯子相接触,很完美;但是四个人碰杯时,任一时刻总会有两个人碰不到杯,非常尴尬。我们自然引出了这样一个问...
连分数的一个性质以及它的一个组合解释
为什么连分数[a1,a2,a3,…,an]和[an,…,a3,a2,a1]的分子是相同的呢?因为这两个连分数的分子表示的是两个左右镜像的棋盘的砖块放置方案数,而两个左右镜像的棋盘本质上是相同...
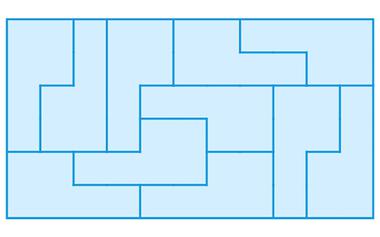
趣题:能否把长方形分成奇数个全等的非长方形小...
能否把一个长方形划分成奇数个全等的小块,并且这些小块不能是小长方形?如果把问题改为偶数个小块,这件事情是很容易做到的。对于奇数个小块的情况,问题显然就没有那么简单了。
趣题:如果每次只增加一个区域的话
著名的四色定理告诉我们,如果一个地图由若干个连通区域构成(没有飞地),那么在给每个区域染色时为了让相邻区域的颜色不同,最多只需要四种颜色就足够了。不过,这个结论成立有一个条件:整个地图已经事...
Lissajous 曲线的动画演示
随着常数m和n的变化,参数方程x=sin(m·t),y=sin(n·t)将会画出一系列漂亮的曲线。法国物理学家Jules Antoine Lissajous曾在1857年研究过这类曲线,因此...
杨辉三角中的自然底数 e
2012年,Harlan Brothers发现了杨辉三角中的一个有趣的事实。不妨把杨辉三角第n行的所有数之积记作sn,那么随着n的增加,sn·sn+2/sn+12会越来越接近e≈2.718。...
最热门
-
莫比乌斯圈和克莱因瓶的美学...
March 08, 2018 -
扭曲的艺术——“怪圈”莫比...
March 07, 2018 -
数学之美|双摆曲线方程
November 10, 2017 -
【全微分】- 图解高等数学...
January 19, 2018 -
【二次曲面】- 图解高等数...
January 19, 2018 -
我眼中的数学之美(更正版)...
March 09, 2018
最多人收藏
-
11:12 AM - March 09, 2018
我眼中的数学之美(更正版)
-
06:22 AM - November 02, 2017
最具争议的12个数学事实,测试和提升...
-
10:32 AM - February 02, 2018
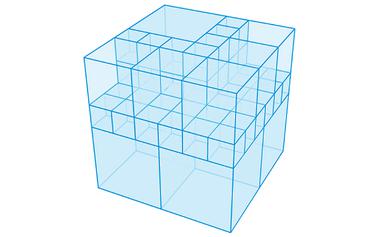
怎样把一个立方体分成 54 个小立方...
-
09:40 AM - January 22, 2018
【投影及其应用】- 图解高等数学 1...
-
10:22 AM - March 07, 2018
爸爸,学数学有什么用?
-
02:08 AM - October 26, 2017
什么是数学建模?